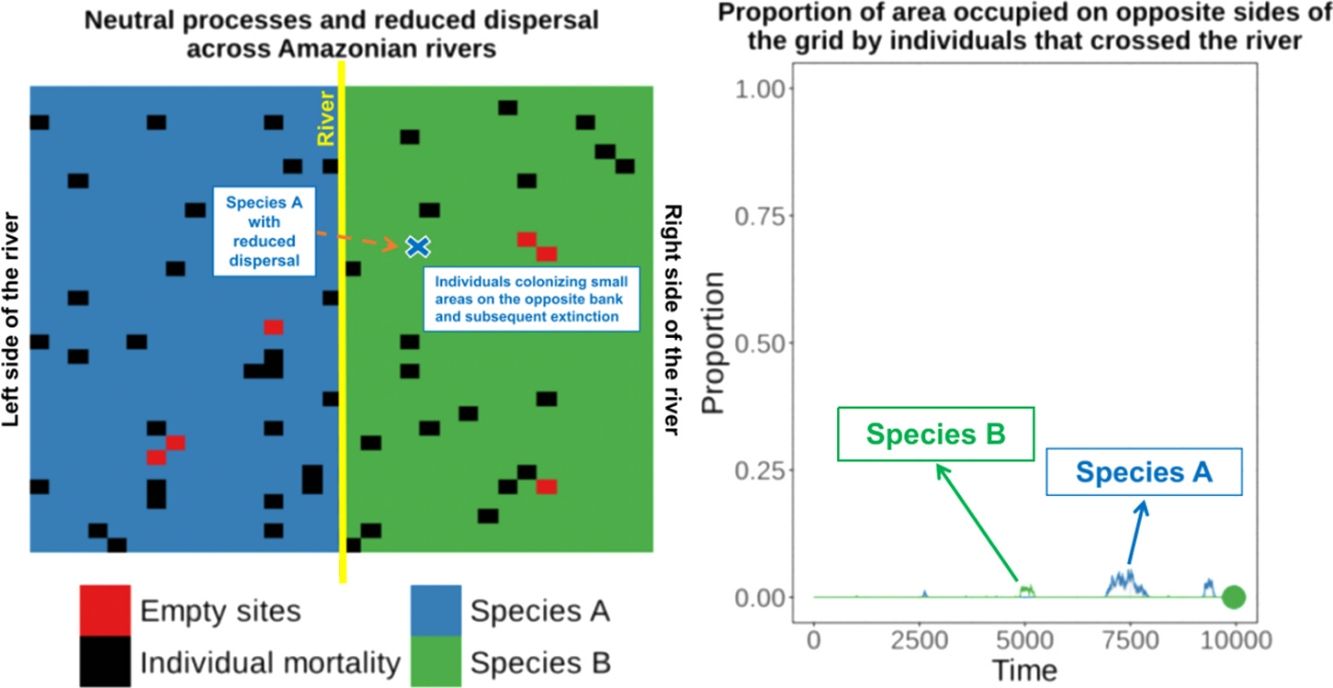
Amazonian rivers are only partial barriers to the dispersal of most species, but they still form the limits between the distributions of many similar species. We show that two competitively-identical species may remain allopatric for hundreds of generations when a river only reduces the chance of a species crossing it. To illustrate this, we developed a two-dimensional cellular automata for two allopatric species under neutral-theory dynamics and recorded the time required for the first extinction of a species and the frequency with which it occurred across replicate simulations. Our results indicate that neutral processes associated with reduced dispersal across rivers can maintain competitively-identical species allopatric for hundreds of generations despite repeated river crossings. These cross-river incursions were rarely successful owing to the low likelihood of a rare invader outcompeting resident populations. This process provides a plausible mechanism for the maintenance of Amazonian biodiversity and may explain the spatial-distribution limits of species caused by large rivers in the Amazon that are not absolute barriers to dispersal.
Allopatric speciation across rivers is a major hypothesis to explain present-day allopatric distributions and regional endemism in the Amazon (see Rull and Carnaval, 2020). Sister species or phylogenetic lineages occurring on opposite banks of large rivers and the boundaries of the distribution of species coinciding with large rivers can be used as evidence that the river subdivided a population to the point of preventing gene flow among individuals and promoted allopatric speciation (Ribas et al., 2012). However, extrapolation of this process based only on present-day species distributions should be done with caution. There is evidence that many species distributions have shifted over time (e.g. Elias, 1992; Graham et al., 1996; Kaustuv et al., 2001), and even sympatric species or lineages could have speciated in allopatry and expanded their ranges into sympatry (Losos and Glor, 2003). More importantly, sympatric speciation followed by dispersal, could result in present-day allopatric distributions (e.g. Graham and Lundelius, 1984), overestimating the importance of allopatric speciation for many taxonomic groups. Haffer (1997a,b) attributed the abutting distributions of many species to secondary contact rather than vicariance speciation owing to the formation of a river.
Recent studies have called into question the frequency with which river-related vicariance events explain allopatry in Amazonia. Several studies have found examples of similar species, sister species or not, which are separated by large rivers, but the evidence indicates that many of these species were not formed by the process of vicariance resulting from the division of a species by the formation of a river (e.g. Byrne et al., 2018; Lynch Alfaro et al., 2015; Hayes and Sewlal, 2004; Moraes et al., 2016). Studies of several morphologically similar and closely related species have failed to support allopatric speciation owing to the formation of a river (e.g. Naka and Brumfield, 2018). Many currently allopatric species separated by rivers have divergence times inconsistent with a river vicariance event (Naka and Brumfield, 2018). In these cases, the river could have been a physical barrier that limited the expansion of species that diverged elsewhere (see Haffer, 1997a,b, 2008), as has been suggested for the robust capuchin monkey Sapajus spp. (Boubli et al., 2015).
The occurrence of sister species or phylogenetic lineages on opposite banks of large rivers without evidence for a vicariance barrier implies that ecological interactions between species could maintain allopatry (Haffer, 1969, 1985). When the river is not an absolute physical barrier, ecologically similar species on an opposite river bank could exclude each other geographically in areas where they come into contact and this pattern might explain what has been described for species in nature. For example, a species of squirrel monkey, Saimiri sciureus, is widely distributed only on the north bank of the Amazon River, but one individual was recorded on the south bank (Mercês et al., 2015). Another squirrel-monkey species, Saimiri collinsi, is widely distributed only on the south bank of the Amazon River, but two individuals were recorded on the northern margin (Mercês et al., 2015). Similarly, the lizard Norops trachyderma is abundant and normally restricted to the right bank of the Tapajós River, but an individual was recorded on the left bank of the river; where the congeneric species, Norops tandai, is abundant and restricted (Moraes et al., 2016).
The species pairs described in the previous paragraph are morphologically similar, and it is uncommon to have morphologically similar congeneric species in sympatry (Darwin, 1859), though competition may be asymmetrical (Twomey et al., 2008). The trumpeter species used to propose endemism areas in the Amazon (Ribas et al., 2012) differ principally in color pattern, which is more important for intra- than inter-species competition, and would presumably compete strongly if in sympatry. Therefore, barriers to dispersal are presumed to be important in generating and maintaining species diversity in the Amazon.
These empirical studies indicate that some individuals of similar species can cross rivers (or could be living in the “wrong” side of the river for many generations at very low densities), but apparently this has not yet resulted in successful invasion and displacement of resident species on that bank. Therefore, the river can be a zone of secondary contact for species that diverged elsewhere. This raises the question of why the individuals of similar species crossing the river did not result in the competitive exclusion of one of the species?
Under the neutral theory of biodiversity (Hubbell, 2001), low dispersal rates can result in some species becoming more abundant by ecological drift and locally dominant due to the low rate of species substitution that is caused by decreased dispersal of individuals. Under neutral theory, the probability of an individual being replaced is given by the relative abundance of the individuals of that species, and this simple process can make a species competitively superior despite the entry of ecologically identical colonizers from places with low dispersal rates. This can result in long-term maintenance of species that are competitively similar. Thus, a large river only reducing the dispersal of a species across the river and not eliminating dispersal, could maintain these species allopatrically distributed over many generations, since the extinction probability of a species is predicted to be a function of population size, resulting in recent colonizers being weaker competitors and more prone to extinction.
To illustrate this process, we developed a two-dimensional cellular-automata model for two allopatrically-distributed species (the expected distribution pattern when the river is a geographical barrier for species dispersal) under neutral-theory dynamics (Hubbell, 2001) and we show that two competitively-identical species may remain allopatrically distributed for hundreds of generations when the chance of a species crossing a large river is reduced. In our simulations, individuals crossed the river but did not spread to the point of eliminating the species occupying the opposite bank in patterns similar to what has been described for species in the nature. This illustrates how rivers can maintain species boundaries, even when the process that generated the species was not a river-related vicariance event.
Material and methodsThe modelTo evaluate whether reduction in dispersal caused by a river is sufficient to maintain species allopatrically distributed on secondary contact even when the river is not a vicariance barrier, we developed a cellular-automata model for two equally-competitive species on a two-dimensional grid, following the general framework of Hubbell’s (2001) neutral theory of biodiversity. To represent the allopatric distribution expected when the river is a barrier, the grid was separated into left and right sides with each side on the grid representing a bank of the river, and each side was occupied by only one species. The river was represented by a constant imposed in the middle of the grid that reduced the chance of either species crossing. We call this constant the degree of river permeability (DsRP).
The model dynamics was set in three sequential steps: (1) local death; (2) pre-colonization - the time between a cell becoming empty due to mortality of an individual and it being colonized or not; and (3) colonization. Each cell on the grid was updated simultaneously based on the local death and colonization probabilities and the sum of individuals of both species in its neighborhood. The neighborhood was composed of a central cell and the cells around it at the preceding time step, according to a set of local rules. The steps and local rules were as follows:
Step 1: Local death (Pld)
Rule 1: Individuals of both species died with probability equal to 0.05.
Step 2: Pre-colonization
Rule 2: Individuals could only colonize an empty cell on the grid after an individual dies.
Rule 3: Individuals of both species had the same chances of colonizing a new cell in the grid (Pc = 0.95). If by chance (1 - Pc), an empty cell remains empty, this cell will be available to be colonized in the next time step.
Step 3: Colonization
Rule 4: The probability of an individual of a particular species colonizing an empty cell was estimated in two steps. First, according to the following formula:
where CspecieX is the contribution of individuals of a particular species in colonizing an empty cell, NindXoppside is the sum of individuals of this species in its neighborhood that were on the opposite side of the grid (i.e. individuals in the left or right side of the river), NindXsamside is the sum of individuals of this species in its neighborhood (individuals who were in the same side of the grid), DsRP is the degree of river permeability, and Sneighb is the number of cells in the neighborhood.In the second step, the probability of a given species colonizing the empty cell was proportional to the contribution of individuals of a particular species in colonizing an empty cell (CspecieX) divided by the sum of the contributions of all species.
As we expected that in nature the chance of a species colonizing an empty cell decreases with distance and with the ability of a species to disperse, we increased the size of the neighborhood to represent different colonizing abilities, assuming that the sum of individuals of both species in its neighborhood is weighted by the distance between these individuals to the empty cell. The distance was defined by the number of squares on the grid between the empty cell and individuals, and the weight was inversely proportional to the square of this distance (inverse square law).
A detailed description and a hypothetical example of model dynamics are included in the supplementary material (Figs. S1 and S2).
Data analysisIn order to show how two competitively-identical species remain allopatrically distributed when the river reduces the chance of either species crossing, we need a better understanding of how ecological interactions are ruled by the neutral theory of biodiversity (Hubbell, 2001). Under the neutral model, a new individual can only establish if another dies and makes space; in that sense individuals are competing for open sites, with advantage being for more abundant species. Thus, a river only reducing the chance of a species crossing makes a species competitively superior despite the entry of new colonizers (more abundant species are stronger competitors in neutral theory). As a result of this process, it is expected that when a river is present, the rate of extinction of the entire population (i.e. the likelihood of being replaced on the landscape) will be lower than in scenarios in which the river is absent.
The scale and neighborhood sizes in the simulation affect the relative abundances of resident and invading populations, which will affect the number of generations to fixation. We investigated 14 different degrees of river permeability (DsRP = 0.01, 0.05, 0.10, 0.20, 0.30, 0.40, 0.50, 0.60, 0.70, 0.80, 0.90, 0.95, 0.99, 1) at two spatial scales (local scale, 32 × 32 grid cells; and regional scale, 128 × 128 grid cells) and five neighborhood sizes (see Fig. S2a for details). Each cellular-automata model was replicated 101 times for 500 generations (10.000 mortality and colonization cycles with Pld = 0.05) and we recorded the rate at which extinction occurred (measured by the number of simulations that resulted in the extinction of one species at the end of the 500 generations). The effect of the magnitude of river permeability on these values was established through cross products property of proportions, comparing their values to those expected with the absence of the river (DsRP equal to 1). Each magnitude value represents in percentage how much higher (positive values) or lower (negative values) the value is when the river reduces the chance of species crossing the river compared to the absence of the river.
To test the expectation that when a river is present the rate of extinction of the entire population will be lower than in scenarios in which the river is absent, we used a one sample t-test (for normal distributions) and Wilcoxon test (for non-normal distributions) to compare the magnitude of extinction rates against the values observed in the absence of the river (DsRP equal to 1). The significance of relationships between the magnitude of extinction rates when the river reduces the chance of either species crossing (i.e. the DsRP constant) was evaluated using linear models. Statistical analyses were used only for the local scale (32 × 32), since no extinction occurred at the regional scale (128 × 128) within 500 generations.
To demonstrate the spatial-pattern dynamics resulting from our simulations; we showed (i) the species distributions on a two-dimensional grid, and (ii) recorded the time required for the first extinction of a species. Under the neutral model, extinction probability of a species is predicted to be a function of population size, and we expected that when a river is present, the number of generations until a species goes extinct on both banks of the river will be higher than in scenarios in which the river is absent (e.g. DsRP equal to 1). The effect of the magnitude of river permeability on these values and the significance of their relationships were evaluated similarly.
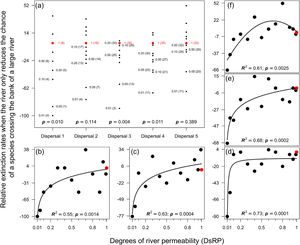
ResultsMagnitude of extinction ratesReducing the chance of species crossing the river lowered the probability of extinction of an entire population in the landscape, especially for species with very low (Dispersal 1), medium (Dispersal 3), and high (Dispersal 4) dispersal abilities (Fig. 1a). The absence of evidence in other simulations (Dispersal 2 and 5) was not enough to exclude the effects of the river reducing the chance of either species crossing on the magnitude of extinction. The relationship expected between degree of river permeability and extinction magnitude was observed in all permeability reductions and dispersal abilities (Fig. 1b–f) for the local scale (32 × 32), but no extinction occurred at the regional scale (128 × 128) within 500 generations.
Magnitude of extinction rates (%) when the river reduces the chance of either species crossing. (a) Comparison of the magnitude of extinction rates with river-barrier (solid black circles) and in the absence of the river (solid red circle). Numbers within parentheses are the number of simulations that resulted in the extinction of one species at the end of the 500 generations and numbers outside parentheses are the degrees of river permeability. The letter p indicates the p-values of a one-sample t-test or a Wilcoxon test. Graphs (b) to (f) show the relationships between number of generations before a species goes extinct and degrees of river permeability. In sequence, each letter represents the abilities of a species to disperse (Dispersal 1–5).
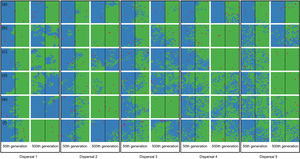
When the chance of a species crossing a large river was reduced to 1%, it was possible to maintain large numbers of allopatrically-distributed individuals for up to 500 generations (Fig. 2a). The individuals crossed the river but could not spread to the point of eliminating the species that occupied the opposite bank (e.g. first column in Fig. 3). The resident species were competitively superior despite the entry of new colonizers that were competitively identical on an individual basis. As a result of this process, the number of generations for a species to go extinct on both banks of the river was high (Fig. S3), and the rate with which it occurred was low (Fig. 1). This pattern was observed especially for species with very low (Dispersal 1), low (Dispersal 2), and very high (Dispersal 5) dispersal abilities (Fig. S3). As degree of river permeability increased (up to about DRP = 0.50), the number of generations to achieve the first extinction decreased in most simulations (Fig. S3b–f). In contrast, as degree of river permeability increased (e.g. see 50th generation in Fig. 2b–f), the individuals crossed the river and gradually spread (e.g. second to sixth column in Fig. 3), making a species competitively inferior in relation to new colonizers, increasing the chance of a species becoming extinct and the landscape to be dominated by a single species (more abundant species are stronger competitors in neutral theory). Consequently, the number of generations for a species to go extinct on the banks of the river was low (e.g. Fig. S3), and the rate with which it occurred was high (e.g. Fig. 1). This effect was greater for some degrees of dispersal (see Dispersal 1–5 in Fig. 2f).
Spatial patterns in simulations at local scale. The blue and green colors represent the two species and red squares represent empty sites on the grid created after individual mortality. The solid line on the middle of the grid indicates where the condition (degree of river permeability) reduced the chance of either species crossing. Letters represent the degrees of river permeability in each row. (a) 0.01; (b) 0.05; (c) 0.10; (d) 0.20; (e) 0.50; e (f) 1.
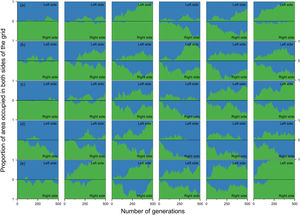
Estimates of the proportion of area occupied on opposite sides of the grid by individuals that crossed the river (right to left side and vice-versa) over generations at local scale. The green area represents individuals descended from individuals that started the simulation on the right side of the grid and blue area the individuals descended from individuals that started the simulation on the left side. Letters represent the abilities of a species to disperse. (a) Dispersal 1, very low; (b) Dispersal 2, low; (c) Dispersal 3, medium; (d) Dispersal 4, high; and (e) Dispersal 5, very high. The columns represent the degrees of river permeability: 0.01, 0.05, 0.10, 0.20, 0.50, e 1; respectively.
The strongest evidence for two competitively-identical species remaining allopatrically distributed when the river reduces the chance of either species crossing, independent of combinations of degrees of river permeability and species dispersal abilities, was observed at the regional scale (128 × 128; Fig. 4); no extinction occurred within 500 generations. However, similar to the patterns observed at the local scale (32 × 32; Figs. 2 and 3), as degree of river permeability increased, and depending on the ability of a species to disperse (Figs. 4 and S4), the chance of a species going extinct and the landscape to be dominated by a single species increased. Hence, results qualitatively similar to those observed in Fig. 1 (the rate at which extinction occurred) and Fig. S3 (time required for the first extinction of a species) could be expected for the regional scale in simulations with more generations.
Spatial patterns in simulations at regional scale. The blue and green colors represent the two species and red squares represent empty sites on the grid created after individual mortality. The solid line on the middle of the grid indicates where the condition (degree of river permeability) reduced the chance of either species crossing. Letters represent the degrees of river permeability in each row. (a) 0.01; (b) 0.05; (c) 0.10; (d) 0.20; (e) 0.50; e (f) 1.
We have only shown the spatial patterns for some degrees of river permeability and generation times in the main text, but Figs. S5–S16 in Supplementary material present detailed results for other degrees of river permeability and generation times.
DiscussionOur results show that simple processes expected under neutral theory (Hubbell, 2001) can result in a large river maintaining two species allopatrically distributed on secondary contact even though the river is not an absolute barrier to dispersal. In a neutral model (Hubbell, 2001), the probability of an individual being replaced is given by the relative abundance of individuals of a particular species, and this simple process makes a species competitively stronger relative to new colonizers simply by the effect of density on competition. Thus, the inclusion of a large river that only reduced the chance of individuals crossing from one bank to another (reducing the entry of new colonizers) was sufficient to maintain two allopatrically-distributed species for hundreds of generations. The process described in our simulation provides a potential mechanism for the maintenance of Amazonian biodiversity, as it allows competitively-similar species to coexist for many generations even though one species would quickly eliminate the other in the absence of the river (Hubbell, 2001).
The discrepancy between the local and regional-scale results highlights the effect of density on competition and how it can maintain two competitively-identical species allopatrically distributed for hundreds of generations when rivers are not absolute barriers. The general pattern was similar to what has been described for species in the Amazon, with dominance of one species on each bank, but with few individuals frequently colonizing small areas on the opposite bank and subsequent extinction of the colonizers on that bank. This is consistent with the proposal of Haffer (1969, 1985, 1997a, 1997b), who discussed the role of Amazonian rivers as secondary barriers for species distributions based on competitive exclusion, rather than complete inability of a species to cross the river, though Haffer (1969, 1985, 1997a, 1997b) did not consider the species to be competitively identical, as in neutral-theory dynamics.
We argue that occurrence of allopatrically-distributed species on either side of a large river need not always be explained by simple stationary process (Case et al., 2005; Holt and Keitt, 2005; Holt et al., 2005) that assume that species are allopatrically-distributed because (i) habitat is not available (e.g. non-flooded flooded areas), and/or (ii) the habitat available is lower-quality (reduced niche limits). The alternative explanation is that the habitat available is separated by physical or biotic factors that weaken colonization rates. Our simulation suggests that when the river reduces the chance of either species crossing, the inability of individuals that cross the river to persist below a critical threshold density makes the immigrant population more vulnerable to extinction and could reduce invasion speeds or even reverse invasions, generating a stable range limit and resulting in large numbers of allopatrically-distributed individuals. Many mechanisms have been proposed for such patterns (see Courchamp et al., 2008) in the absence of adaptive evolution (e.g. see Andrade-Restrepo et al., 2019; Kanarek and Webb, 2010), but our analyses cannot distinguish between them.
The present simulation shows how rivers may act as effective secondary barriers as suggested by Haffer (1969, 1985, 1997a, 1997b). It is likely that sister species or phylogenetic lineages have originated on opposite banks of large rivers without river-related vicariance events, then spread rapidly by chance (Hubbell, 2001), either due to the absence of a competitor (Case et al., 2005) or predator-prey interactions (Kubisch et al., 2014) within an area bounded by rivers (often called endemism centers) until they meet somewhere near the river. When they meet, both species would remain allopatrically distributed because it is difficult for new immigrants to establish themselves and to reproduce (e.g. Gascoigne et al., 2009) within the interfluve occupied by another species. This mechanism does not assume that the species have accumulated sufficient divergence to exploit different niches. The absence of divergence makes the species ecologically similar, but they remain allopatrically distributed for long periods because of competitive exclusion and dispersal limitation (e.g. Gutiérrez et al., 2014; Pigot and Tobias, 2013, 2015; Weir and Price, 2011). This process could maintain competitively-identical species allopatrically distributed for hundreds of generations, giving opportunity for genetic drift or adaptation to different environments resulting in evolutionary differences that prevent fertile crosses between species (Luzuriaga-Aveiga and Weir, 2019; Nosil, 2012).
A number of studies (e.g. Fecchio et al., 2017; Ferreira et al., 2017; Naka et al., 2012) have concluded that large Amazonian rivers increase Amazonian biodiversity throughout vicariant speciation without refuting plausible alternative conclusions. Models based on vicariant speciation, where rivers are assumed to have divided previously continuous populations, have been used to justify interfluves between major rivers as endemism areas that can be used in conservation planning when detailed information about most taxa is lacking (Caro and O’Doherty, 1999; Da Silva et al., 2005). However, several studies indicate that the large rivers are insufficient to explain the spatial-distribution limits of species and to indicate endemism areas for most phylogenetic lineages (Santorelli et al., 2018). The effectiveness of rivers as dispersal barriers also varies longitudinally, being greater near the mouth than in the upper reaches (Godinho and da Silva, 2018). The role of large rivers as geographical barriers works for some taxa better than others (e.g. Paula Lima et al., 2020) and in some rivers more than others (Nazareno et al., 2019), and does not work well for highly-dynamic rivers, as there are several cases in which river-capture processes (e.g. Ruokolainen et al., 2019; Albert et al., 2018) could have resulted in species with small populations on the side of the river occupied by a congeneric species.
Models based on vicariance work well for some organisms, especially large birds (Ribas et al., 2012), but less so for others (Santorelli et al., 2018). To improve conservation models, it will be necessary to have more complex models that include dispersal modes, rates of evolution of different taxa, the potential for competitive exclusion and differences in the degree of sexual selection. All these focus on deterministic differences among taxa, but our simulations show that neutral processes based on relative abundances may be important to maintain and possibly generate diversity across rivers. Reduction in the amount of habitat available to taxa through deforestation will affect relative abundances and the processes that we have described, with implications for conservation planning well beyond the identification of vicariance speciation.
In conclusion, our simulation study shows that neutral processes and reduced dispersal across Amazonian rivers present another mechanism by which present-day allopatric distributions of similar species may arise without invoking a river-related vicariance event. To differentiate among hypotheses to explain allopatric distributions, we strongly recommend the use of the protocol proposed by Naka and Pil (2020). However, there is a need for more understanding of the dispersal characteristics of organisms and factors that limit river crossing, especially under scenarios of climate change that may reduce river flows, alter dispersal patterns, and change relative densities of species on opposite banks.
Data availability statementData are available on the PPBio site <https://ppbio.inpa.gov.br/> and Data ONE (Brazilian Program for Biodiversity Research - PPBio - Western Amazon & Center for Integrated Studies of Biodiversity in the Amazon - CENBAM).
Declaration of interestsThe authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
This study was supported by the Coordenação de Aperfeiçoamento de Pessoal de Nível Superior - CAPES; Coordenação de Pesquisas em Biodiversidade – CBIO of the Instituto Nacional de Pesquisas da Amazônia - INPA; Programa de Pós Graduação em Ciências Biológicas (Biologia de Água Doce e Pesca Interior); Centro de Estudos Integrados da Biodiversidade Amazônica (INCT-CENBAM) and the Program for Biodiversity Research in Western Amazonia (PPBio-AmOc). We are especially thankful to the Texas Advanced Computing Center (TACC) at The University of Texas at Austin for providing High Performance Computing resources that contributed to the research results reported in this paper. URL: http://www.tacc.utexas.edu.