As threats to the marine environment are increasing over time, the United Nations aims to protect 30% of the ocean by 2030 as one of its sustainable development goals. In order to maximize the ecological benefit for the ocean, a coordinated global effort in marine protected area (MPA) planning is necessary. In this context, ecological connectivity between areas should be considered. Connectivity has been integrated in several previous MPA designs however this usually requires exhaustive larval information (which may not be readily available) and/or complex ocean current simulations (which may be arduous at the transnational scale). In this study, we developed a simple passive drift model of larval dispersal as an alternative approach to integrate connectivity in MPA design. By doing so, we determined larvae source and sink areas between the Philippines and Taiwan, and recorded the time it takes for the virtual larvae from the Philippines to reach the sink zones in Taiwan. We used integer linear programming to identify areas best suited for protection in the Philippines, and found that Batanes, Philippines seeds Green Island and Orchid Island in Taiwan. Travel time of the virtual larvae was estimated to range between 7 and 12 days. We also demonstrate that the integrated approach to maximize habitat area and minimize larvae travel time yields promising results for marine conservation. This approach could be instrumental in marine conservation planning, especially in the formulation of a transboundary MPA network.
The International Union for Conservation of Nature (IUCN) defines marine protected areas (MPAs) as “areas of the ocean set aside for long-term conservation aims.” These areas are regulated and restricted from human activities to safeguard and restore marine biodiversity (Abesamis et al., 2006; Angulo-Valdés and Hatcher, 2010; Kerwath et al., 2013). They have also been proven to fuel neighboring waters as a result of the increase in population density, not only with reef fishes (Abesamis and Russ, 2005; Tupper, 2007) but also with lobsters (Goñi et al., 2010). Marine organisms do not move only in a limited distance, but they also travel further away until they reach a suitable habitat where they can settle. For this reason, some MPAs were scaled up into MPA networks organized for a common conservation objective.
The importance of a global effort to protect the ocean has been widely investigated. Several studies suggest that partnerships and collaborations among countries and stakeholders to form an MPA network would result in more promising, efficient, and effective MPAs (Chen and Keshavmurthy, 2009; García-Barón et al., 2019; Laffoley et al., 2008; Sala et al., 2021). However, most of the MPAs already established worldwide are not ecologically connected, and some are not even supplying larvae to their own exclusive economic zones, suggesting that these MPAs may not be strategically placed (Andrello et al., 2017).
Connectivity has been globally known to be crucial in marine conservation planning (Magris et al., 2016, 2017; White et al., 2010). It is usually demonstrated with biological techniques like otolith sampling (Di Franco et al., 2015) and DNA analysis (Chen and Keshavmurthy, 2009; Liu et al., 2010), which are costly and time-consuming. For this reason, biophysical dispersal models were developed to predict connectivity on a larger scale (Andrello et al., 2017; Wood et al., 2014). These models have been established on the premise that ocean currents strongly influence genetic variation among populations (Muñoz-Ramírez et al., 2020; White et al., 2010). Despite this, according to the review conducted by Balbar and Metaxas (2019), only 11% of MPA designs consider connectivity due to the complexity of creating such models (Burgess et al., 2014). This field, however, is making quick progress from theoretical approaches (Berglund et al., 2012; Kininmonth et al., 2011; Smith and Metaxas, 2018) to coupling biophysical models with prioritization tools like Marxan (Magris et al., 2017; Muenzel et al., 2022). Nevertheless, since these methods are mostly species-specific, they may therefore have a bias towards certain species (Bradbury et al., 2008) while ignoring other relevant species in the ecosystem (Byrne, 2012). These methods may also require specific biological parameters like larval behavior and planktonic larval duration (PLD) which may not be widely and easily available (Balbar and Metaxas, 2019; Treml et al., 2012).
The Kuroshio Current, which flows from the eastern side of the Philippines through the Luzon Strait to the east Taiwan channel, is known to be a strong and stable current that influences marine biodiversity in the Philippines, Taiwan, and Japan. In fact, Chen and Keshavmurthy (2009) suggested that Taiwan could be a connective stepping stone for coral communities in this region while Liu et al. (2018) studied the connectivity patterns of megamouth sharks in the area. Bayliff et al. (1991) also showed that the area between the Philippines and Taiwan is the spawning ground of bluefin tuna. Despite these studies highlighting the importance of this region, there is still no initiative known, so far, for the protection of this region. In this regard, we developed a simple passive drift transport model based on ocean currents to design an MPA network that maximizes natural habitat area and optimizes connectivity in this region.
To properly assess connectivity, we define it as the larvae originating from a well-represented habitat that successfully reach the sink zone, with the assumption that the sink zones are also composed of suitable habitats (Allen Coral Atlas, 2020; Chang et al., 1989, 1992; Chen, 1999) where larvae can settle and thrive. In other words, a cell with good connectivity should have a dense habitat area and a short travel time for a higher chance of the larvae to reach the sink zones. Specifically, we computed the time larvae travels from its point of origin in the Philippines to the sink zones in Taiwan by drifting on the ocean current. We then minimized the travel time on the premise that: (1) the shorter the travel time, the lesser the chances for larvae to encounter predators or other environmental threats that affect its survival; (2) prolonged larval phase may decrease the likelihood of larval settlement due to storage of energy (Graham et al., 2008); (3) most species settle when they find a conducive environment and suitable substrate (Rodd et al., 2022); and (4) climate change (Kendall et al., 2013) may result in an increase in sea surface water temperature which was shown to reduce PLD (Green and Fisher, 2004; McCormick and Molony, 1995; Rankin and Sponaugle, 2011).
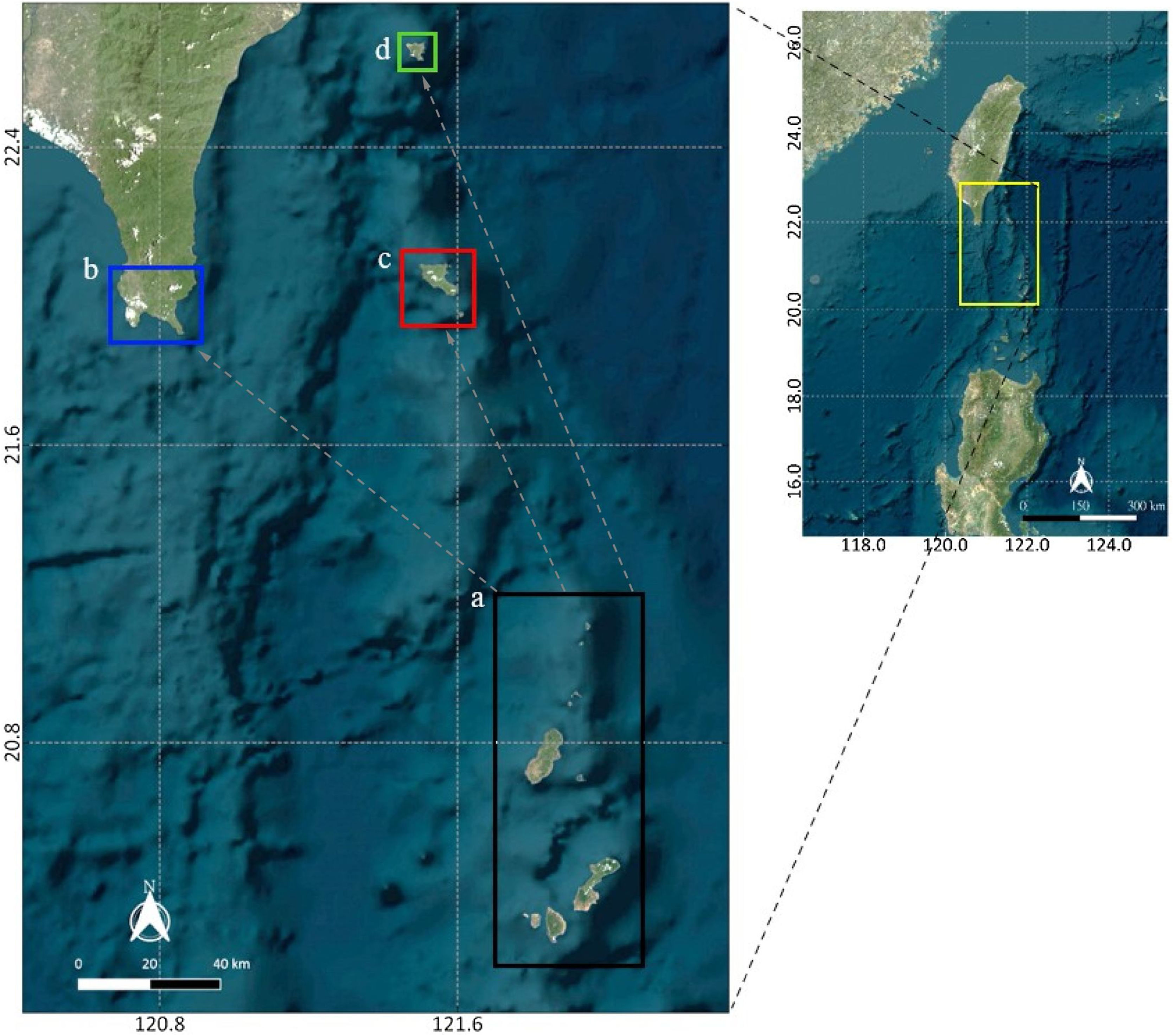
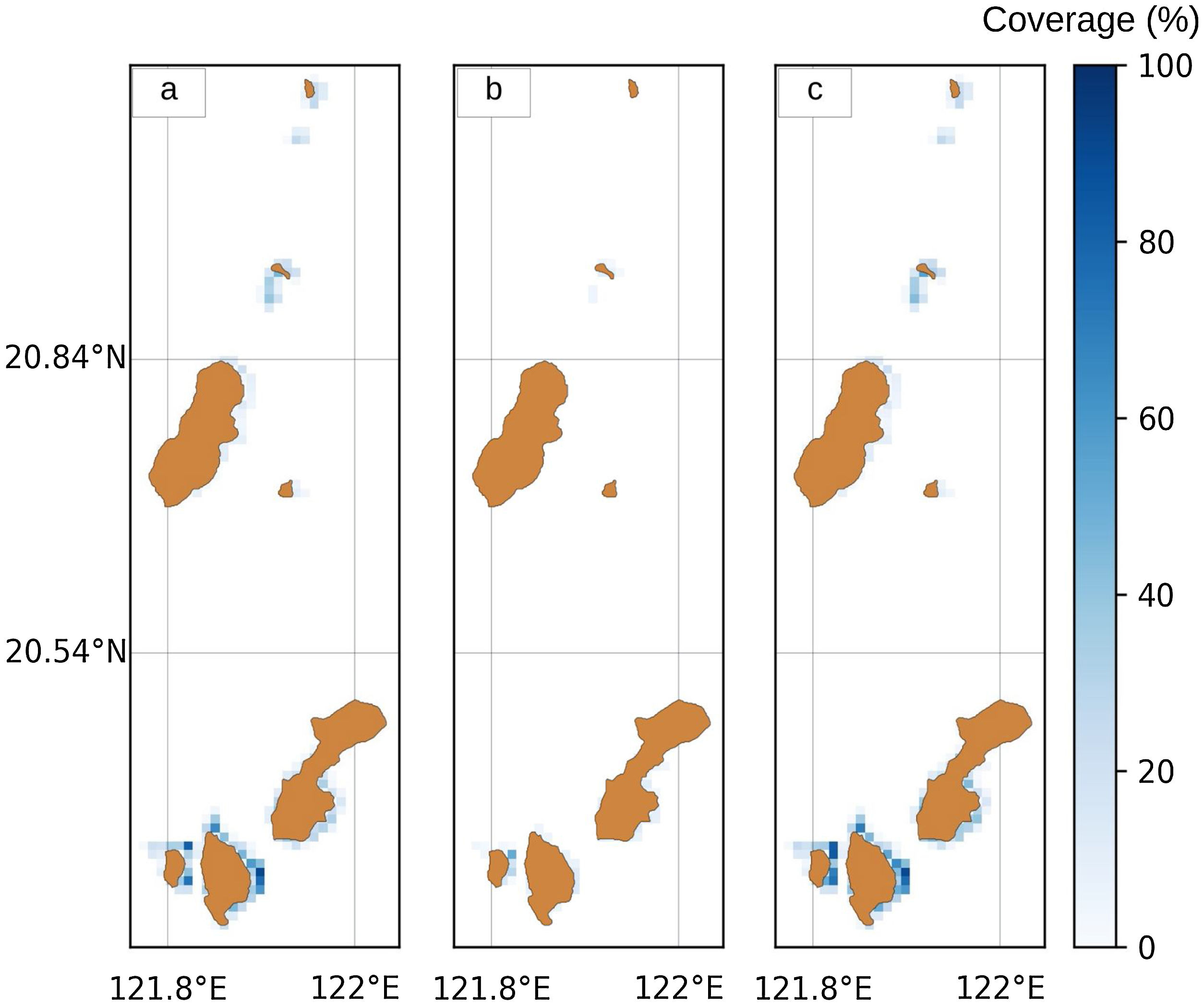
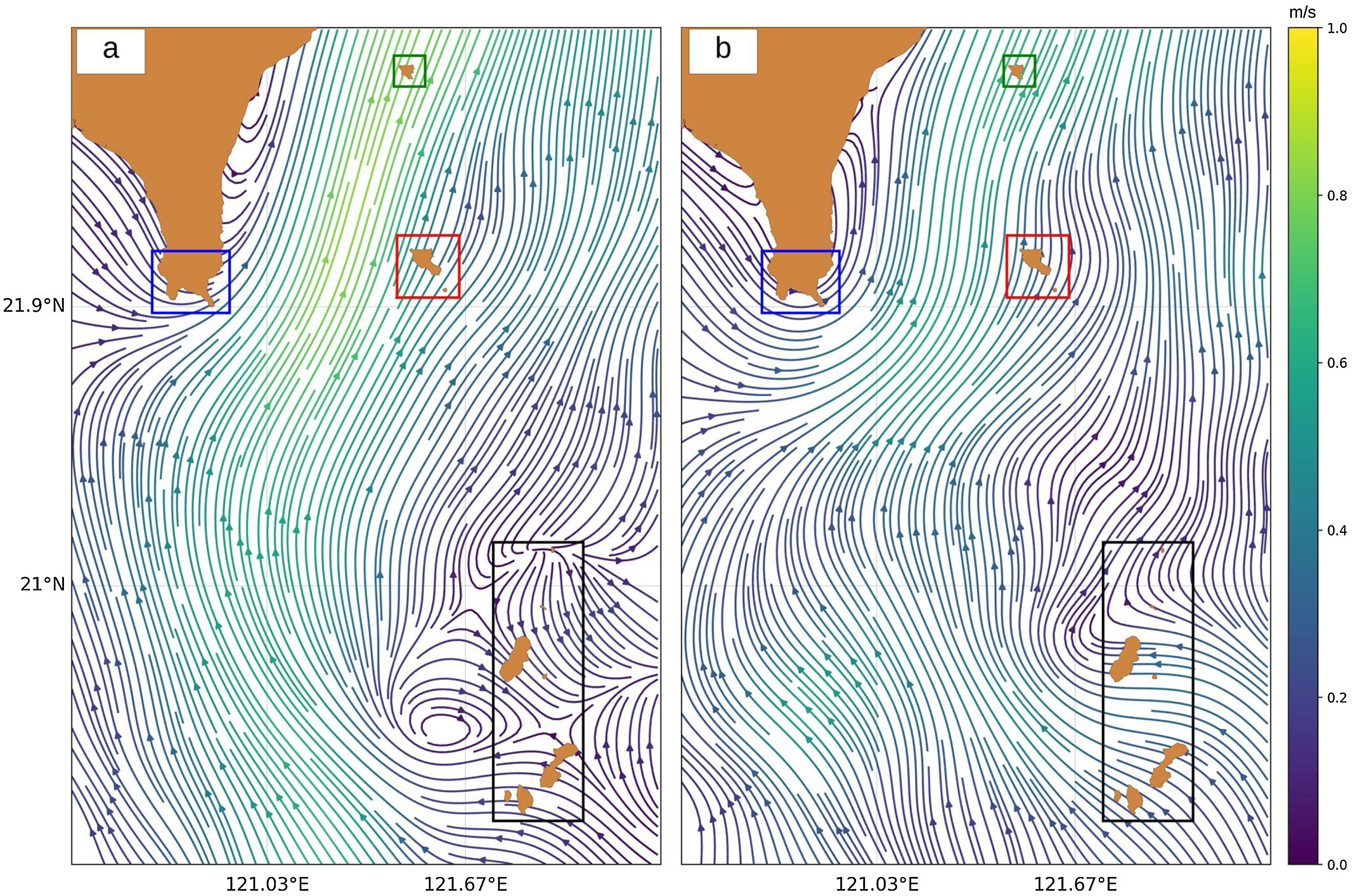
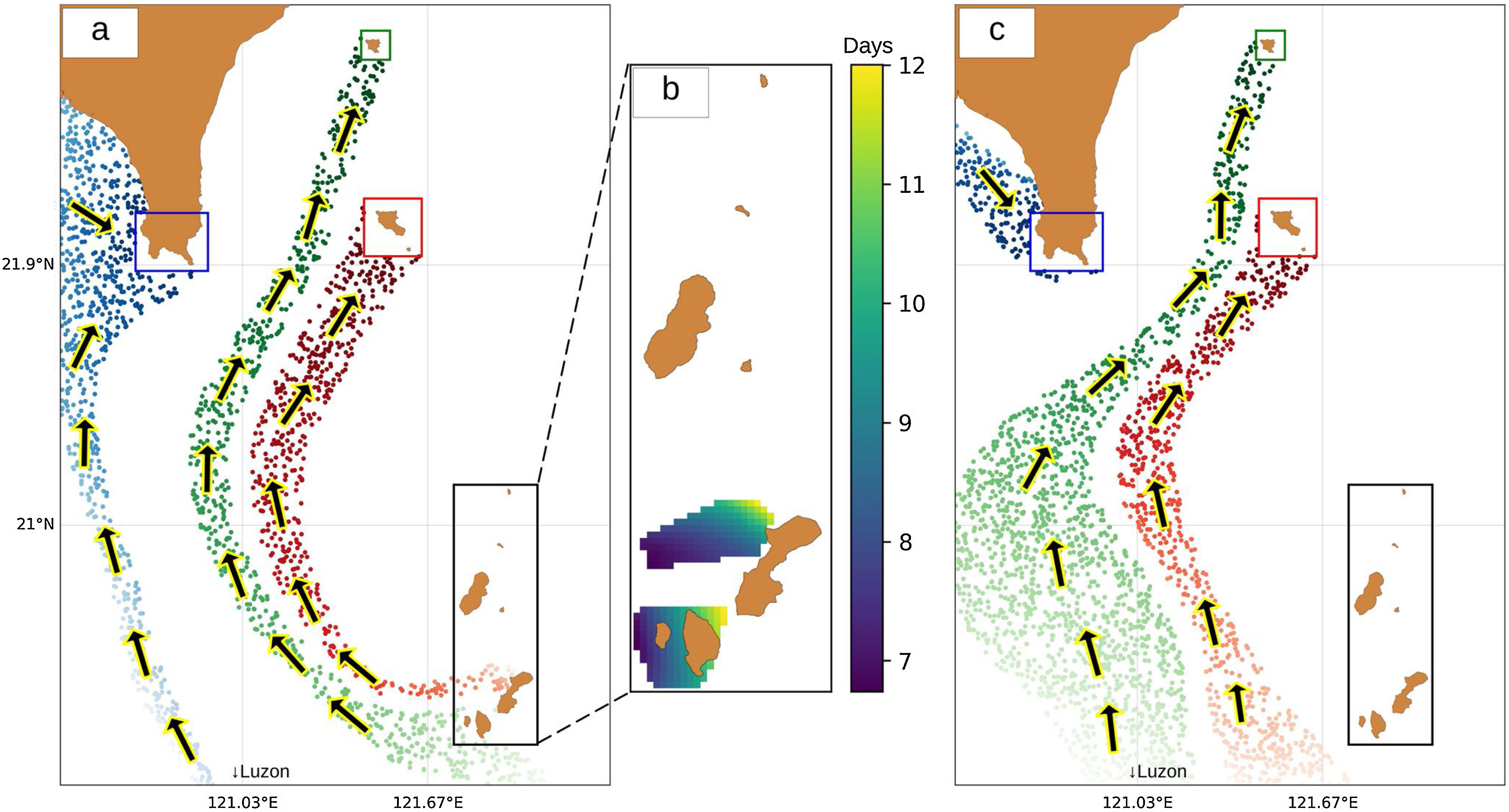
Study area and methodologySpatial extentThe spatial extent of this study encompasses four sites within Taiwan and the Philippines: one in the northernmost part of the Philippines (Batanes) and three in the southernmost part of Taiwan (Kenting, Orchid Island, and Green Island). Since Batanes is in the upstream of the Kuroshio current, it was assumed that this area seeds larvae to Taiwan. Therefore, a strategic approach would be to protect this area to benefit the countries in the downstream of the Kuroshio current. For this reason, Batanes was chosen to be the main planning region where the selection of MPAs occur (Fig. 1a). This planning region of 300,000 ha is composed of 3000 cells (100 rows and 30 columns) of 100 ha area each. Random starting points for virtual larval dispersal were generated throughout the study area, and their trajectories were simulated using 27 years of acoustic doppler current profiler (ADCP) data. Initial locations for larvae that successfully reached Kenting (Fig. 1b), Orchid Island (Fig. 1c), and Green Island (Fig. 1d) were recorded along with their travel time.
Data preparation and processingGeo-referenced spatial habitat data for coral reefs and seagrass beds in 2019 were obtained from the Provincial Environment and Natural Resources Office (PENRO) in Batanes, Philippines. These datasets were rasterized in a 100 × 30 matrix (Fig. 2a and 2b). Since both coral reefs and seagrass beds are important for ecological connectivity (Dorenbosch, 2006; Nagelkerken et al., 2008), we considered the aggregate area of both habitats for future use in the model Fig. 2c).
Ocean current data from 1991 to 2018, obtained through an ADCP, was acquired from the Ocean Data Bank (ODB), Taiwan. The ADCP device is installed in Taiwan’s research vessels to measure the speed and direction of the ocean current, which is then stored in a database managed by ODB. Since coral reefs and seagrass beds are usually found in shallow waters (Guannel et al., 2016; Jagtap, 1998), the data records were filtered to exclude deep (>100 m) ocean currents. The filtered data records were then averaged and interpolated linearly for the two following seasons: summer (April to September) and winter (October to March), as shown in Fig. 3.
Model formulationTransport model for larval dispersalThe connectivity of a population in marine areas is often associated with the ocean current, (Andrello et al., 2017; White et al., 2010) as reef-related larvae are mostly planktonic (Chacon-Gomez et al., 2013; Lobel and Robinson, 1986) and their swimming ability is limited (Hata et al., 2017). With critical swimming speed (U-crit) estimated around 0.12 m/s (Fisher et al., 2022), tropical larval and juvenile fish are drift according to the ocean current’s direction and speed (Werner et al., 2007) which greatly influences their dispersal patterns (Muñoz-Ramírez et al., 2020; Sun et al., 2020). This study is therefore not species-specific, as it was assumed that since the Kuroshio current is (on average) an order of magnitude faster than the average U-crit, it was safe to assume that larval dispersal and settlement were highly dependent on (1) the strength and direction of marine currents (Cowen and Sponaugle, 2009; Scheltema, 1986) and (2) the availability of a suitable habitat in the settlement (sink) zone, regardless of the species considered.
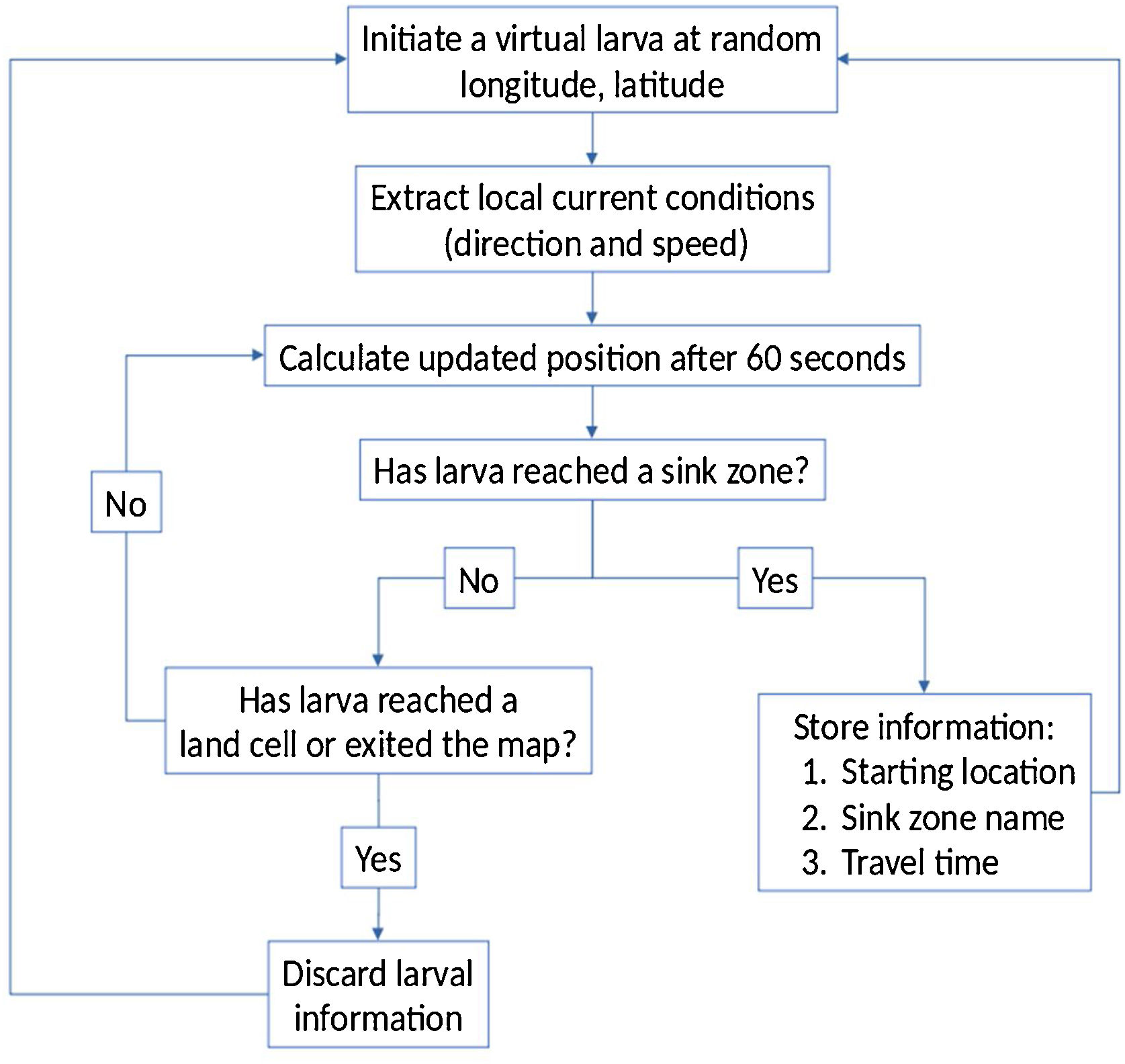
We developed a passive drift transport simulation model using Python. We generated 10,000 random virtual larvae within the study area and updated their geographic coordinates every minute according to the averaged/interpolated currents shown on Fig. 3. Starting locations for virtual larvae that successfully reach the sink zones (Kenting, Orchid Island, and Green Island) were recorded along with their travel time, while starting locations that led elsewhere were discarded. A flowchart of the process is shown on Fig. 4.
To validate that these sink zones have suitable habitats for settlement, we checked the Allen Coral Atlas (2020), a global database of coral reefs and found that these areas are mostly composed of corals (46% in Green Island, 44% in Orchid Island, and 66% in Kenting). Other references also studied the distribution of scleractinian corals in this region (Chang et al., 1989, 1992; Chen, 1999) and Soong et al. (2003) studied the recruitment patterns in these areas.
The travel time was then normalized (a value of zero corresponding to the minimum travel time and a value of one corresponding to the maximum travel time) to ease further addition to habitat cover in the optimization model. A value of 2 was then specified as a penalty for cells in Batanes that don’t connect to the sink zones in order to prevent the selection of these cells.
Optimization model for MPA selectionThere are two main algorithms used for systematic conservation planning: simulated annealing (SA) and integer linear programming (ILP). Marxan, developed by Ball et al. (2000) and is the most commonly used software for marine conservation planning, uses SA. Because of the sophisticated interface of this software and easy access to online trainings, it is a very popular tool among marine spatial planners. However, several studies have revealed the drawbacks of SA as compared to ILP such as the cost-effectiveness, the time of simulation, and the sub-optimality of the solution due to the stochastic nature of its underlying algorithm (Cheng et al., 2015; Schuster et al., 2019). The ILP model we developed is derived from the land acquisition model established by Wright et al. (1983) where he also introduced the concept of compactness to measure how fragmented the selection is. This is determined by the number of external borders, referred to as the boundary length (BL) and specified as a constraint in this study.
To show how connectivity can inform MPA planning, we generated two models with different objective functions: M1, to maximize the total area covered by both corals and seagrass beds, and M2, to maximize the total area covered by both habitats while minimizing the travel time of the virtual larvae. Habitat values were normalized between zero (no habitat) and two (100% cover) so that their importance is the same as travel time, whose values range from zero (shortest) to one (longest) and two (no connection).
The models described in Table 1 were developed in GAMS (General Algebraic Modeling Language) and were solved using the CBC (COIN-OR Branch and Cut) solver.
Mathematical formulation of optimization models M1 and M2.
| Model 1 (M1)Maximize habitat area representationMaximizeZ=∑i(ai+bi)xiSubject to:Cells∑ixi=MCompactness∑i∑j∈Ti(Pij+Nij)≤BLxi−xj−Pij+Nij=0 ∀i,j∈TiPij+Nij≤1 ∀i,j∈Ti | Model 2 (M2)Maximize habitat −travel timeMaximizeZ=∑i(ai+bi)xi−∑icixiSubject to:Cells∑ixi=MCompactness∑i∑j∈Ti(Pij+Nij)≤BLxi−xj−Pij+Nij=0 ∀i,j∈TiPij+Nij≤1 ∀i,j∈Ti |
Where Z is the objective value; i and j are the indices for the planning units where i is the selected cell while j is the adjacent cell; a is the percentage of coral reef area; b is the percentage of seagrass area; c is the normalized time it takes for the virtual larva to reach the sink area; x is a binary variable indicating whether the ith grid is selected for protection, where 1 is selected and 0 is not; M is the number of cells; Ti is the set of cells adjacent to cell i; Pij and Nij is the measure of compactness as explained by Wright et al. (1983) where Pij is 1 if xi = 1 and xj = 0, 0 if otherwise and Nij is 1 if xi = 0 and xj = 1, 0 if otherwise; BL is the number of external boundaries defined as follows:
BminM≤BL≤BmaxM
BmaxM=4M
BminM=4⌊M⌋+2t
where BminM and BmaxM are the lower and upper limit on the number of possible external borders, respectively and t is a parameter defined in the following equations:
t=0 if M-⌊M⌋2=0
t=1 if M<⌊M⌋2+⌊M⌋+1
t=2 if M>⌊M⌋2+⌊M⌋+1
⌊M⌋=integer part of M
M1 represents the traditional approach of habitat maximization. The model is anchored with the following assumptions: (1) that habitat area can act as a proxy for the biomass of coral reefs and seagrass beds species (Ward et al., 1999), and (2) protection of a denser habitat area is beneficial for biodiversity (Margules and Pressey, 2000). With that, this model is formulated with the objective function to maximize the total habitat area subject to a given boundary length.
However, in order to have an effective marine reserve, it is also important to consider that the selected MPA is connected to possible settlement sites (Andrello et al., 2017). For this reason, M2 was developed to represent our proposed integrated approach to include connectivity. M2 seeks to maximize habitat area while minimizing larvae travel time. For illustration purposes and since the area with habitat is limited, these two models were set to select only 10 cells equivalent to 1000 ha and BL ranging from 14 km to 40 km.
ResultsLarval dispersal and MPA selectionOur results show that the southern part of Batanes seeds larvae to Orchid and Green Island only in summer (Fig. 5a) while there is no connection during winter (Fig. 5c). It was also found that Kenting does not receive virtual larvae from Batanes but may be connected to the Babuyan islands of northern Luzon, Philippines. The interpolated travel time from Batanes to Orchid and Green Island in summer ranges from 7 to 12 days, with larvae originating from the dark blue pixels in Fig. 5b taking 7 days to reach the sink zones, and larvae originating from the yellow pixels taking 12 days. One of the possible organisms that spawn during this time are corals from the family of Faviidae and Acroporidae (Jamodiong et al., 2018; Vicentuan et al., 2008).
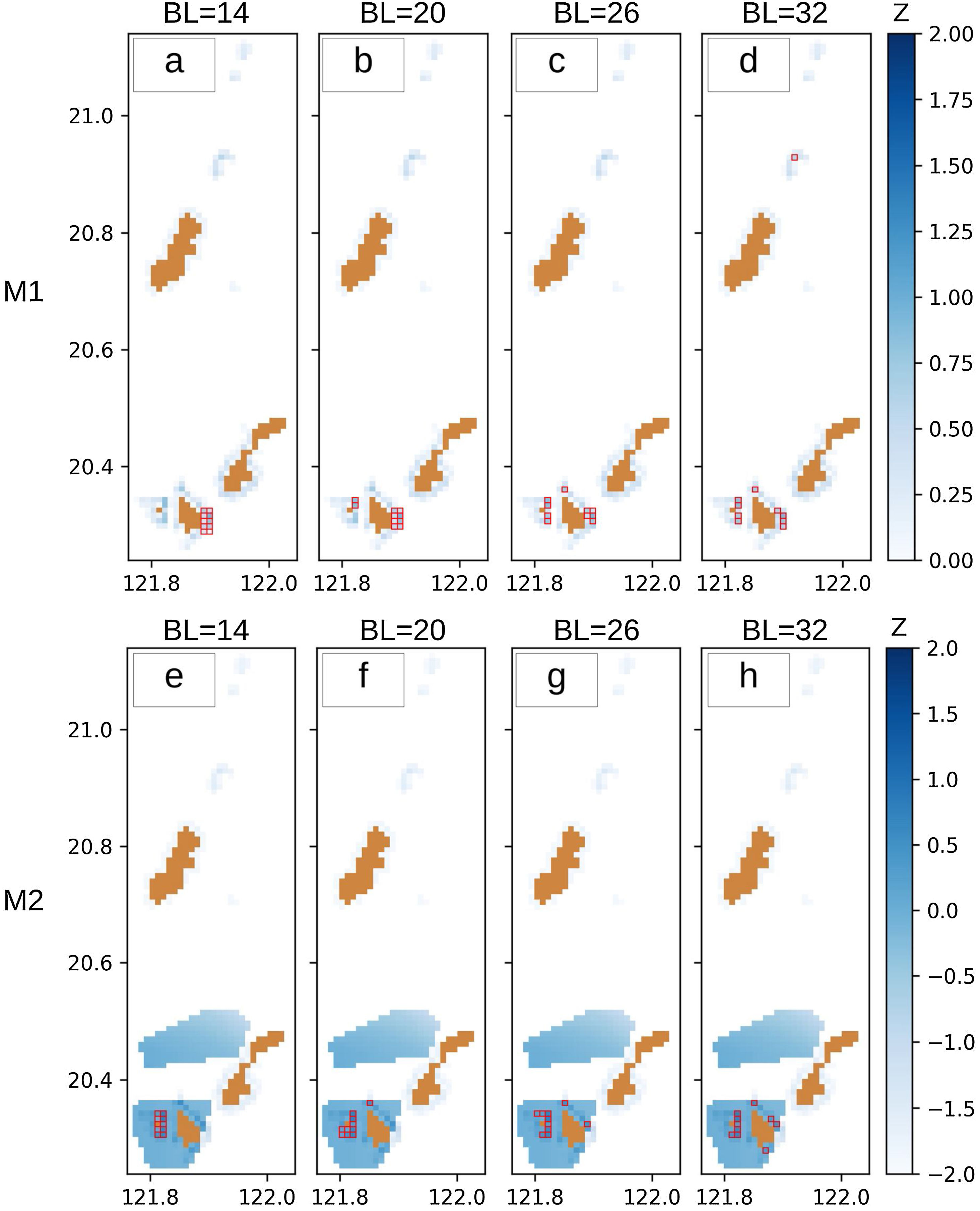
Fig. 6 shows the MPAs selected by the optimization models we developed: Fig. 6a–d for the traditional approach (M1) and Fig. 6e–h for the integrated approach (M2). M1 selected ten cells that have the maximum total habitat area depending on the specified boundary length. For example, the most compact scenario (BL = 14, Fig. 6a) selected an MPA with a habitat area of 489.15 ha which is equivalent to 13.74% of the total habitat area in the whole Batanes region. Although some cells on the southwestern part of Batanes have the greatest habitat area, these are not part of the selection because of the compactness constraint that requires the ten selected cells to be arranged in a rectangle. When disaggregation is allowed (BL = 32, Fig. 6d), the selection favors individual cells with greater habitat area. The sum of the habitat area in this fragmented selection is equal to 725.90 ha (20.39%).
When M2 is specified to have the same weights for habitat and travel time, the solution exhibits a totally different selection when high compactness is required (BL = 14, Fig. 6e). This is due to the shorter travel time on the southwestern side of Batanes (Fig. 5b). However, when greater disaggregation is allowed (BL = 32, Fig. 6h), the MPA selection for M2 tends to favor more of the same cells than M1, with a 60% similarity. This relative convergence of M1 and M2 under low compactness requirement is due to the structure of the dataset with six cells having both a high natural habitat area and short travel times.
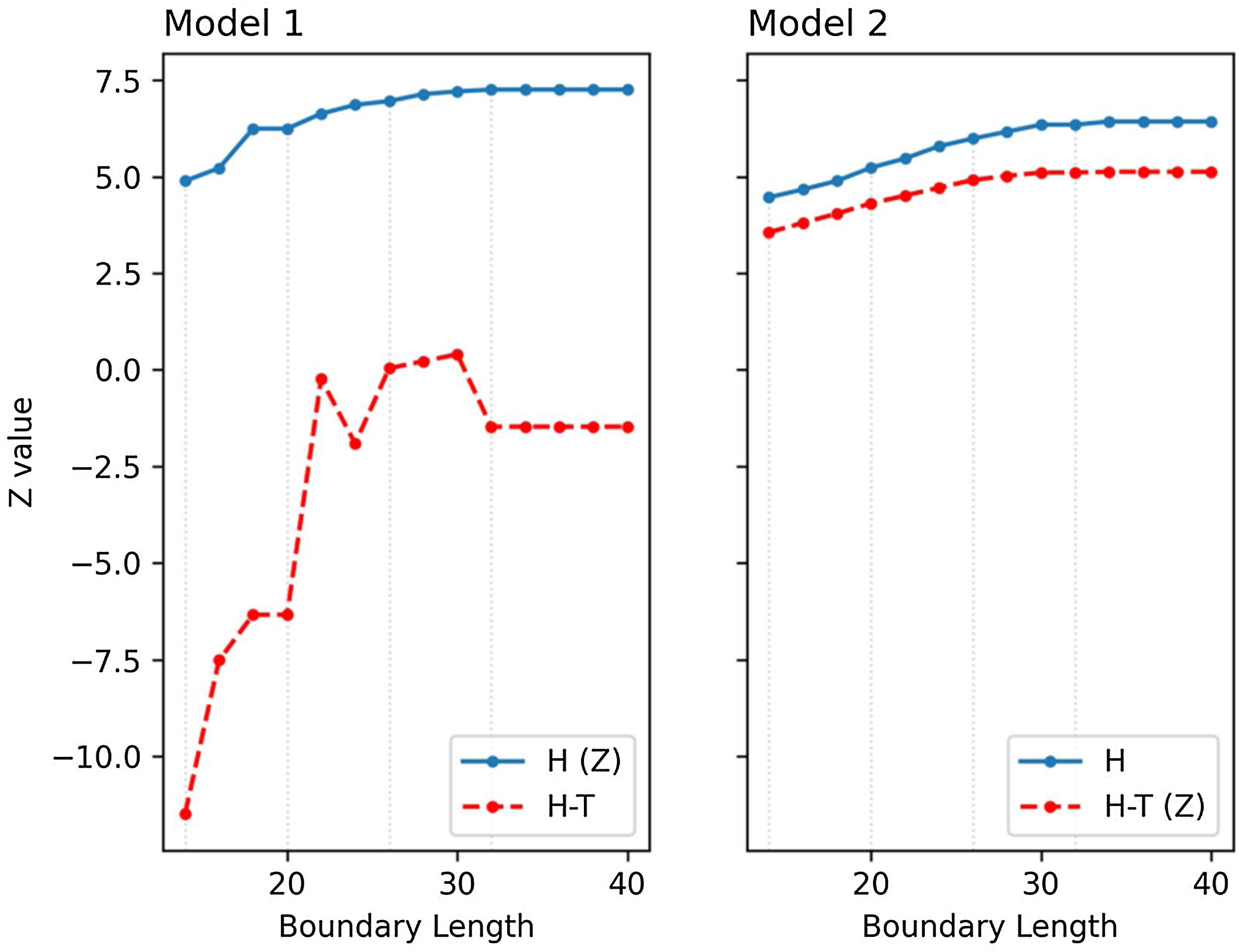
Opportunity costTo assess the difference between M1 and M2, we computed habitat (H) and habitat minus travel time (H-T) in both models. The objective function of M1 is H while for M2 it is H-T. To compare the behavior of both models with respect to its objective function, we manually computed the counterpart of the objective function in each model from the selection of the other model and plotted accordingly in Fig. 7. Indeed, despite excluding travel time in formulating M1, we still cannot ignore the fact that each selected cell in the M1 solution (Fig. 6a–d) has a corresponding travel time. With this, we can calculate H-T manually in order to compare its behavior with M2.
Z (objective) values (H (Z) and H-T (Z)) in comparison to their computed counterpart (H and H-T) from the selection of the other model across different boundary lengths (BL) in (a) model M1 and (b) model M2. Dotted grey lines highlight the Z values of the solutions presented in Fig. 6 for BL = 14, 20, 26, 32.
Fig. 7 shows that habitat values (H) are lower in M2 as compared to M1, but the integration of travel time in the objective function allows for much higher H-T values in M2, due to the fact that most of the selected cells in M1 do not connect and therefore suffer a penalty. The difference of H between M1 and M2 (the deviation from the compromised solution of M2 and the reference optimality of M1) can be interpreted as the opportunity cost of integrating connectivity into MPA planning.
Furthermore, this study also explored the opportunity cost of compactness which is determined by BL. This BL has always been considered crucial in MPA planning (Chen et al., 2015; Cheng et al., 2015; Fraschetti et al., 2009) which may usually cause some trade-offs with cost (Ball et al., 2000) or biodiversity (Chen et al., 2015). This trade-off between multiple objectives is common in optimization models (Eskelinen and Miettinen, 2012). A more compact MPA is usually preferred to a disaggregated one as it is thought to encompass more fish which can enhance the spillover effect (Laffoley et al., 2008). McLeod et al. (2009) summarized previous studies on the size of MPA networks and came to a conclusion that most studies suggest that the bigger the size of the MPA, the better. The reason for this is to protect higher marine habitats to shelter a larger portion of marine organisms that depend on these habitats for survival (Green et al., 2007; Mora et al., 2006; Palumbi, 2004). Our results show that given a specific size of 10 cells, a more compact MPA (BL = 14) protects a lesser percentage of habitat area (13.74%) as compared to a disaggregated one (BL = 32, 20.39%), highlighting the opportunity cost of compactness. This result contributes to the increased understanding of strategic approaches in MPA design (Cabral et al., 2020; Margules and Pressey, 2000; Sala et al., 2021).
DiscussionConsiderations toward MPA planningThe duration at which larvae survive in the water column differs greatly between species. For reef fishes, it was reported to range from 18 to 73 days (Victor and Wellington, 2000) while scleractinian coral larvae may survive up to 244 days before settlement (Graham et al., 2008). The computed travel time of the virtual larvae in the MPA selection shown in Fig. 6 (e–h) ranges from 7.08 to 7.75 days. This shows a higher chance that when a marine organism with a PLD greater than 7 days spawns in the southern part of Batanes, it is still viable upon reaching Orchid or Green Island. This result can hopefully spark a dialogue for both the Philippines and Taiwan to co-develop a transboundary MPA network.
Since this study is working on that idea, it is also important to consider the individual circumstances of the local players to ensure the effective management of each MPA site. This is where trade-off analysis comes into play. Despite the knowledge that a disaggregated MPA protects a higher habitat area, in the setting of a local scale (which can be the case in Batanes), it is likely more difficult to manage a disaggregated MPA due to the demands of management efforts (Chen et al., 2015), such as monitoring of MPAs (Abesamis et al., 2019), installation and replacement of buoys or markers, and patrolling which would be both financially costly and time-consuming when moving from one site to another.
Moreover, the trade-off analysis (Fig. 7) is essential when different sectors have contrasting preferences such as when environmentalists may require full protection or the protection of a greater habitat area, while fishers may argue that fishing regulations are already enough to be effective (Catalano, 2016). Alternatively, MPA managers may prefer a single compact MPA, while the national government prefers to protect as much habitat area as possible to achieve its conservation objectives. The tension that might arise from these situations can be eased with an effort to consider the views of both stakeholder groups (Harris et al., 2019), by showing the trade-off curve and providing the pros and cons of having different objectives to the decision-makers so they can weigh these factors according to their preference. The participation of these stakeholders is critical in the effective management of MPAs (Lucrezi et al., 2019) as well as in bridging the gap between science and implementation (Mills et al., 2020).
Implications for a transboundary MPA network in the KuroshioMPA networks are now being considered globally as a tool to enhance marine biodiversity and connectivity, and promote fishery management as they have been shown to be more effective than isolated MPAs (Palumbi, 2004; Metcalfe et al., 2015). The United Nations aims to protect at least 30% of the ocean by 2030. To aid in this objective, strategic MPA planning should be considered to efficiently maximize the benefit from marine waters. Transboundary MPA networks (Sala et al., 2021) and connectivity (Andrello et al., 2017) have been key considerations in this strategic global effort. However, the inclusion of connectivity in MPA design may require a wealth of biological information for both genetic approaches and biophysical modeling such as larval behavior and dispersal traits which may be unavailable, especially for large areas such as a transnational scale. This study proposes a simpler alternative for biophysical modeling to integrate connectivity in a possible future transboundary MPA network between the Philippines and Taiwan, with the aim of contributing to this global coordinated effort through M2, by which the potential source areas with higher chances of connectivity from Batanes to Orchid and Green Island were identified. Since we only mapped the well-represented habitats in the source (spawning) areas, our next step would be to determine which specific cells in the sink zones these source cells are connected to and how suitable they are for settlement. Settlement sites in Batanes should also be identified as larvae could be coming from the eastern side of the Philippines where a healthy coral reef is located (Nacorda et al., 2017). Similarly, the role of Taiwan as a stepping stone for coral connectivity along the Kuroshio current could be investigated by extending the study to Okinawa, Japan.
Furthermore, it is recommended, for future studies to: (1) include threats like coral bleaching and other anthropogenic activities to the model, (2) incorporate socio-economic features in the planning process such as fisheries and tourism, (3) expand the complexity of larval dispersal by adding stochasticity to the ocean current, and (4) validate this approach with empirical data.
This study could be a preliminary effort to establish a transboundary MPA network between the Philippines and Taiwan where negotiations among countries and other stakeholders should be considered, especially when deciding how the MPAs should be designed. Another related issue is the evaluation of the benefits of conservation in the Philippines for Taiwan, the willingness of local communities to support such a program, and the exploration of potential mechanisms to ensure equity and benefit sharing between these two countries.
ConclusionThis study promotes the importance of designating MPAs in areas with high connectivity to maximize the long-term benefit of larval dispersal which eventually fuels coral reef communities in other areas. The model we described is particularly useful in designing large-scale MPA networks where ocean currents are strong and stable, where data on larval dispersal may not be readily available, and conservation is not only limited to certain species. The simplicity of the model makes it a good alternative to more complex approaches based on biophysical modeling and can easily be adopted in marine conservation planning. We hope this can serve as a preliminary (or validation) phase of scoping for MPA networks, not just between the Philippines and Taiwan, but eventually along the whole Kuroshio current, or anywhere else in the World. Given the global state of marine resources, it is high time we try to harness natural forces such as marine currents to design more efficient MPA networks.
Declarations of interestThe authors report no declarations of interest.
This study was funded by the Ministry of Science and Technology, Taiwan under the project entitled, “A National Ocean Governance Geared towards International Regimes (1/4)” [MOST 111-2425-H-110-001]. Our utmost appreciation goes to the Provincial Environment and Natural Resources Office (PENRO) of Batanes, Philippines and Ocean Data Bank (ODB) of the Ministry of Science and Technology, Taiwan for providing us with data for the conduct of this study. Government agencies in the Philippines, specifically the Department of Environment and Natural Resources - Biodiversity Management Bureau (DENR-BMB), and Bureau of Fisheries and Aquatic Resources – Region 2 (BFAR 2), are also acknowledged for their support. Our sincere thanks as well to Mr. Jared Vicentillo and Mr. Ronald Fidel for their assistance, and the anonymous reviewers for their time and effort devoted to improving the quality of this paper. Dr. Emma Ballad, Ms. Alita Sangalang, Dr. Vera Horigue, and Dr. Rene Abesamis are also acknowledged for their insightful comments both during and after the first author’s master’s thesis defense.