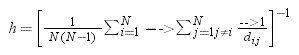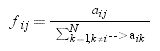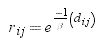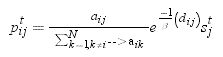Landscape homogenization, caused by monocultures, can provide optimal conditions for the spread of crop pests. Increasing habitat heterogeneity and complexity within landscapes could slow pest spread. A next step in understanding the role of habitat heterogeneity in affecting pest spread is to understand how landscape features directly and indirectly affect spatial infestation patterns. We developed a spatial network approach to explore how landscape complexity, generated by forest patch cover, affects the pest spread in agricultural landscapes. As a studied system, we used information on the spatial distribution of traps and dispersal distance of the sugarcane borer Diatraea saccharalis (Lepidoptera: Crambidae) from a sugarcane agro-ecosystem in Brazil. Network analysis reveals that modeling pest spread was an outcome of both direct and indirect pathways connecting sugarcane fields. Therefore, using only information about the direct and indirect pathways of the spatial network and the initial focus of infestation, we were able to predict with nearly 80% accuracy the most susceptible sites to pest spread in the simulated landscape. By adjusting parameters such as pest mobility, and interaction with landscape features, our model can simulate different agricultural systems and pest behaviors, showing that forest cover can be used to control pest occurrence and that direct and indirect pathways in spatial networks can be used as a predictive tool to manage the pest spread in agricultural landscapes.
Landscape simplification is a hallmark of the Anthropocene (Albuquerque and Gonçalves-Souza, 2022). Croplands and pastures now cover nearly half of the Earth’s habitable surface, a scenario primarily driven by agricultural intensification and land conversion due to food demand (FAO and ITPS, 2015). Landscape degradation due to food production negatively affects 3.2 billion people worldwide and costing ∼10% of the global gross product in reduced biodiversity and ecosystem services (United Nations, 2020). Paradoxically, the ecosystem services that are lost due to intensive agriculture, such as pest control, could increase yields and/or decrease farming costs (Paredes et al., 2021; Tamburini et al., 2020). Indeed, crop damage by pests costs to farmers a large amount of resources (Paredes et al., 2021). For example, a minimum of US$70 billion is spent on pest control per year globally (Bradshaw et al., 2016). To increase food production, farming practices worldwide have intensified the use of pesticides (Rey Benayas et al., 2008). Thus, a strategy that combines conservation efforts with food security is a global priority (Leclère et al., 2020). In this sense, a range of natural pest control strategies exist, which focus on controlling pests using natural enemies and disrupting their dispersal across the landscape (Rusch et al., 2016).
Natural pest control improves in landscapes with greater habitat diversity and structural complexity (Paredes et al., 2021; Martin et al., 2019; Dainese et al., 2019). Landscape complexity is enhanced in landscapes where crops are interspersed with habitat patches (Boetzl et al., 2020). These patches may support larger and more resilient populations of natural enemies (Dainese et al., 2019; Boetzl et al., 2020; Bianchi et al., 2006; Chaplin-Kramer et al., 2011; González et al., 2020) which foster the ecosystem service of natural pest control (Montoya-Pfeiffer et al., 2020; Morandin et al., 2016; Silva et al., 2015; Aristizábal and Metzger, 2019; Barral et al., 2015). For instance, in sugarcane fields, natural vegetation patches support interactions between pests and their natural enemies, reducing pest populations (Rivera-Pedroza et al., 2019; Santos et al., 2018). The abundance of predatory functional groups among ants and birds was found to be lower within sugarcane fields compared to vegetation patches (Rivera-Pedroza et al., 2019). This has significant implications for the provision of essential predation services targeting key pests in sugarcane crops, such as Diatraea spp. (Rivera-Pedroza et al., 2019) Moreover, coffee plantations in landscapes with greater vegetation cover or closer to forest edges, are less likely to have coffee borer (Hypothenemus hampei) infestation due to pest control by ants (Aristizábal and Metzger, 2019). In addition to the number of habitat patches and coverage, their spatial arrangement in the landscape is important for the levels of pest control (Aristizábal and Metzger, 2019).
By 2050 it is estimated that the range size of invasive terrestrial invertebrates, including crop pests, will increase on average by 18% (Bellard et al., 2013). Thus, it is important to develop modeling approaches to understand, manage and prevent pest dispersal across landscapes. Modelling approaches for pests have focused on population dynamics, interactions with natural enemies, invasion risks, and environmental drivers affecting pest dispersal (Tonnang et al., 2017). A challenge, however, is to develop approaches to predict how landscape features affect pest spread. This challenge is critical in regions dominated by monocultures, as pest dispersal is rapid but may be affected by small changes in landscape complexity. Indeed, habitat patches potentially disrupt the pest spread: (i) as a physical barrier preventing the dispersal of some pest species across the landscape; and (ii) as a reservoir of predators and parasitoids that can depress pest populations.
Here, we developed an approach integrating network science with mathematical modelling to understand how landscape complexity may affect the pest spread across intensively managed agricultural landscapes. We parameterized our analyses with data from a large-scale sugarcane agroecosystem in São Paulo State, Brazil. Brazil is the largest net exporter of cane sugar and sugarcane fields in Brazil cover approximately 9.1 million hectares (Companhia Nacional de Abastecimento, 2016). The sugarcane landscape is a mosaic composed of intensively cultivated sugarcane stands interspersed with patches of native and restored vegetation. In these landscapes, sugarcane plants are attacked by the sugarcane borer moth Diatraea saccharalis (Botelho and Macedo, 2002; Dinardo-Miranda et al., 2012a; Myers, 1932a) – species used as a showcase of the study. In a sugarcane landscape, Diatraea spp. may avoid forest patches as a strategy to protect themselves from natural predators (e.g., ants and birds) (Rivera-Pedroza et al., 2019). To understand how landscape features (e.g., native and restored forest cover) can influence the pest spread we explored: (1) what is the role of forest patches in the structure of the spatial network through which pests spread; (2) how the spatial network structure affect the pest spread dynamics; and (3) can direct and indirect pathways among sites in the spatial network be used to predict the most vulnerable sites to pest spread in the landscape. We hypothesized that the distribution of forest patches alters the structure of the spatial network by introducing or removing nodes and edges that change the connectivity and pathways available for pest movement, potentially creating new pathways or barriers for pest spread. Moreover, modifications in the spatial network structure due to the distribution of forest patches will result in altered pest spread dynamics, specifically by either slowing down the rate of spread through increased vegetation or facilitating spread through newly created pathways. Finally, the analysis of direct and indirect pathways within the spatial network will allow for the identification of sites that are most vulnerable to pest spread, with sites exhibiting high connectivity in the spatial network being more susceptible to becoming infested.
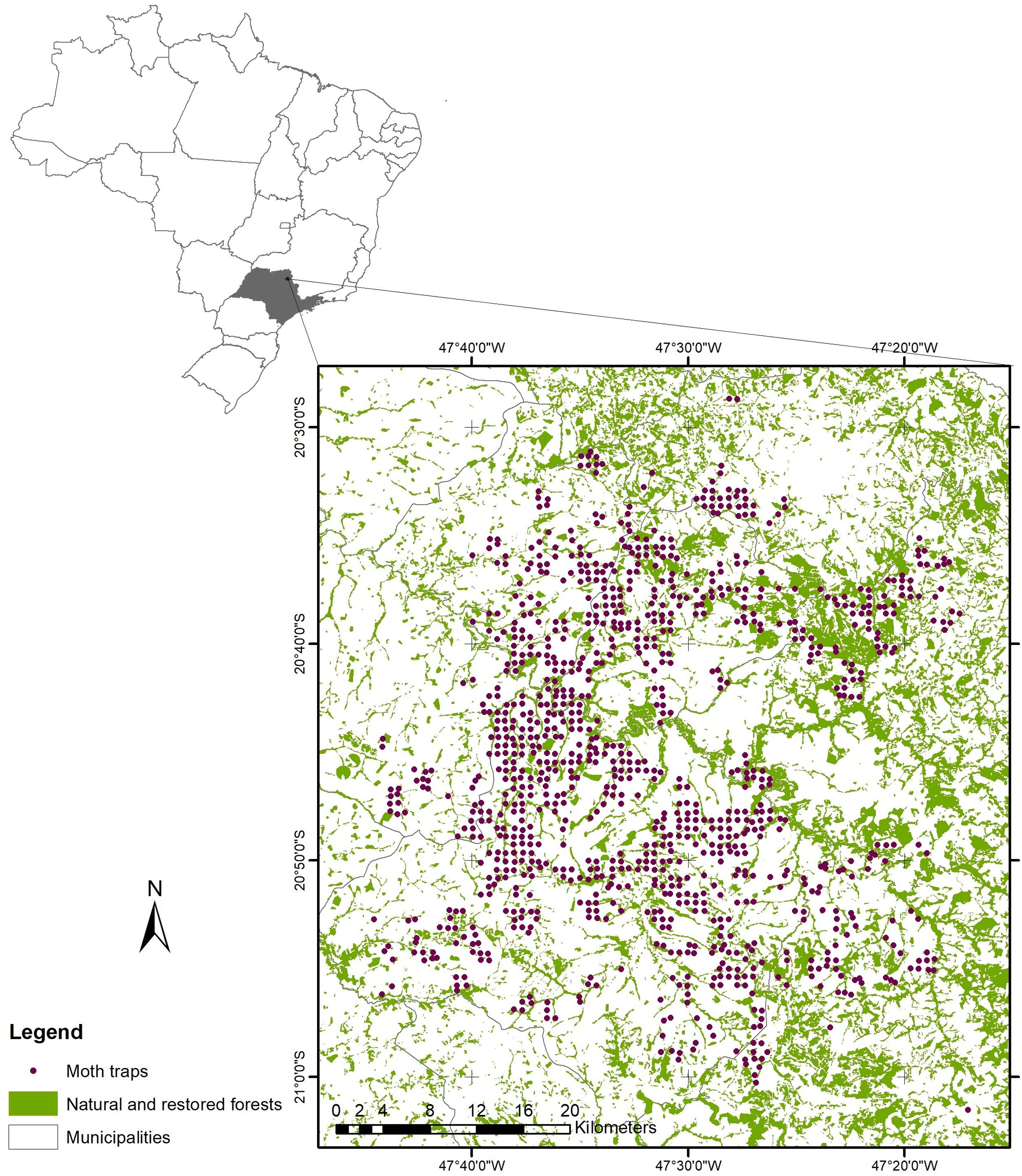
Materials and methodsStudy regionThe study landscape is in an ecoregion in northeastern São Paulo State, Brazil (20°46’S, 47°34’W) situated between two vegetation domains: Atlantic Forest and Cerrado (savanna) (Fig. 1). The region is considered one of the most threatened in Brazil, with high biodiversity and endemism but also widespread anthropogenic pressures (Ribeiro et al., 2009). Non-crop vegetation accounts for 15% of land cover, and is restricted to small fragments of secondary forest vegetation in different stages of succession, and wooded savanna (cerradão) (Kronka et al., 2005). Some of these habitats have been actively restored, as defined by the Native Vegetation Protection Law, which have been planted by landowners (Rodrigues et al., 2011; Sparovek et al., 2012). Patches of natural vegetation are interspersed in a matrix dominated by sugarcane (>90%), but with some Eucalyptus spp. and Pinus spp. plantations, fruit crops (Citrus spp.) and pasture (SigRH, 2016).
Sugarcane borer (Diatraea saccharalis)The sugarcane borer Diatraea saccharalis (Fabricius, 1794) is a species of moth in the family Crambidae. The original plant hosts of the larvae are likely aquatic and semi-aquatic grasses (Myers, 1932a; Myers, 1932b), yet it has since colonized maize and sugarcane (Francischini et al., 2019) and is now considered one of the most important pests in sugarcane crops (Botelho and Macedo, 2002; Dinardo-Miranda et al., 2012a; Myers, 1932a). Damage is caused by its larvae in the internodes of the culms which may lead to plant death, reducing total productivity (Botelho and Macedo, 2002; Dinardo-Miranda et al., 2012a; 2014). According to several studies, 1% of borer infestation on sugarcane crops causes ∼1.5% reduction in stalk production, ∼0.5% reduction in sugar production, and ∼0.3% reduction in alcohol production (Dinardo-Miranda et al., 2012b; Arrigoni, 2002).
The entire larval lifecycle of the moth occurs in sugarcane. Eggs are oviposited in the leaves and larvae hatch 4–9 days later. The larvae initially feed on the leaves for 7–15 days, after which they descend into the stem. After 40 days in the stem the larvae pupate, and then approximately 10 days post-pupation adults emerge, surviving for approximately 3–8 days (Sandoval and Senô, 2010; Holloway et al., 1928). The whole cycle takes 44–120 days and 4–5 generations are completed per year (Sandoval and Senô, 2010). As adults, females remain relatively stationary (Pérez, 1964) and attract males by releasing pheromones that are carried on the wind. As such, male moths of D. saccharalis generally disperse more frequently than females, reaching a maximum distance of 800 m in flight (Caixeta, 2010). The adults have nocturnal habit and, in general, remain in the same area in low population size as long as there is no competition for food. However, greater dispersion occurs under food restrictions (Mendez et al., 1978).
In Brazil, generalist ant species contribute to the natural biological control of eggs and early larval stages of D. saccharalis (Rossi and Fowler, 2004; Oliveira et al., 2012a). However, the active management mainly focuses on biological control involving the larvae of the exotic parasitoids Cotesia flavipes (Hymenoptera: Braconidae) (Botelho and Macedo, 2002) or Trichogramma galloi Zucchi (Hymenoptera: Trichogrammatidae) (Consoli et al., 2010), combined with chemical control (Erler, 2010), which incur significant cost to the sugarcane companies (Rossi and Fowler, 2004).
Trap dataWe compiled an annual georeferenced dataset (2019–2020) of D. saccharalis presence/absence across the study region (1,089 sites approximately 680 m apart) from pheromone trap data collected by a sugarcane company located at the northeastern of São Paulo state, Brazil. Briefly, delta traps with three virgin female moths (from laboratory breeding populations) were placed on the leaves of sugarcane plants to attract adult males of D. saccharalis which are then trapped on the sticky floor surface. Traps were removed after three days and the occurrence of D. saccharalis was recorded (Oliveira et al., 2012b). This monitoring was completed three times a year and is used to inform management of D. saccharalis (Trematerra, 2012). We used data on forest cover, georeferenced trap records of the pest D. saccharalis, and simulated forest management scenarios to generate spatial networks in which we model the pest spread.
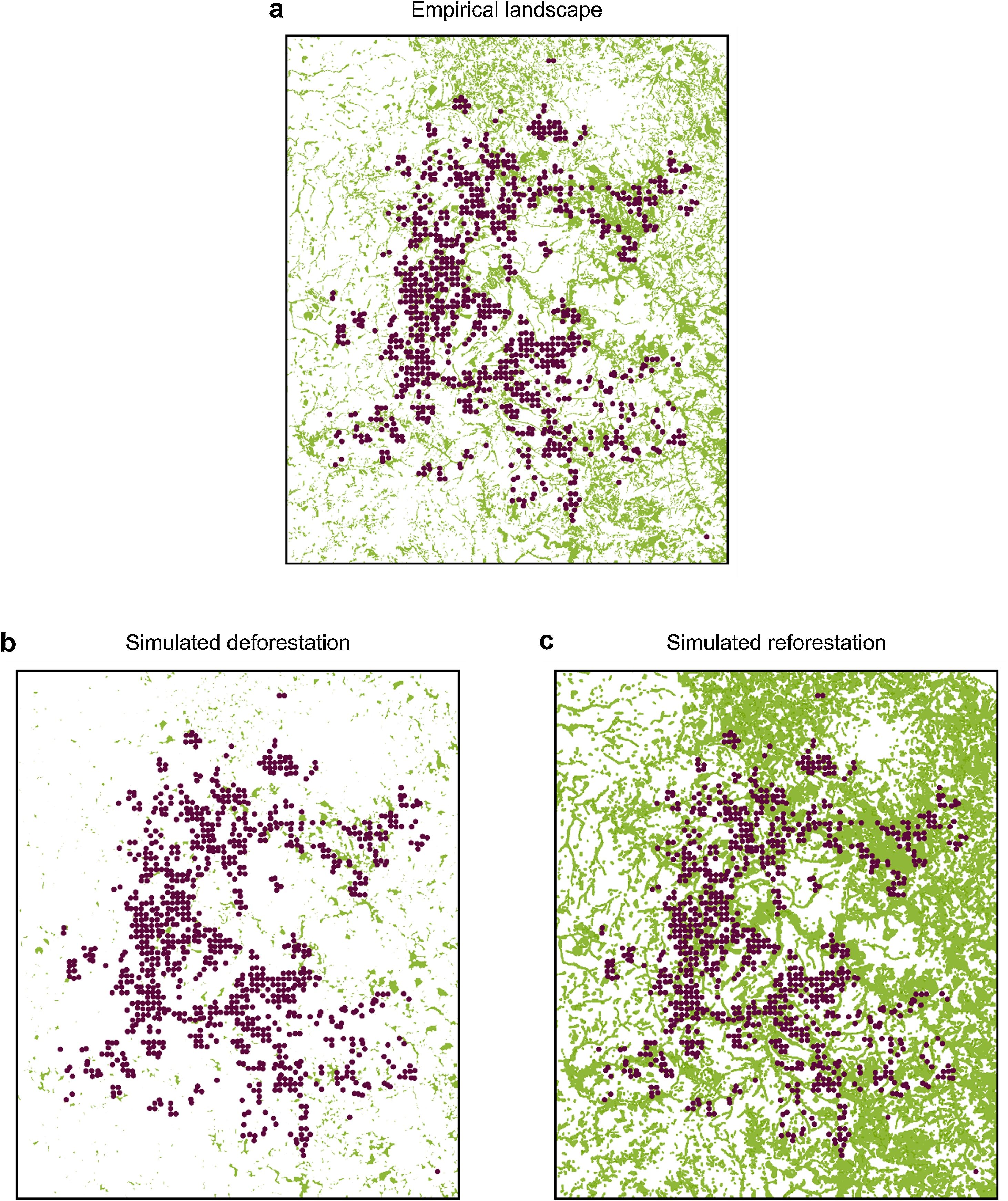
Forest coverForest cover data for the study region was obtained from the Brazilian Annual Land Use and Land Cover Mapping Project (Collection 5 of the MapBiomas project, http://mapbiomas.org). Data provided by MapBiomas are produced from the pixel-per-pixel classification of Landsat 8 satellite images (30 × 30 m resolution) from 2019. From the MapBiomas data for the study site, we extracted shape files with the category “forest” and reprojected the coordinates from Latitude-Longitude to UTM, datum SIRGAS 2000. For the study, forest includes remaining forests, second growth forests and restored forests. We calculated the percentage of forest cover (natural or restored forests) across the landscape as the ratio of the area of forest polygons to the total area of the study region. We used the percentage forest cover of our study landscape from MapBiomas (16.7%) as a basis to simulate different scenarios. We assumed that forested habitats represent barriers to pest dispersal because (1) of increased abundance and diversity of natural enemies as they provide more ecological niches (Rivera-Pedroza et al., 2019; Santos et al., 2018) and (2) can be avoided by pests as a defensive strategy against natural predators for different species of Diatraea, such as ants and birds (Rivera-Pedroza et al., 2019). We simulated forest patch management by altering forest cover in the landscape by either expanding or contracting existing forest patch cover (Fig. 2). We incrementally change the area of each forest polygon in all dimensions. To do so, we used the st_buffer function from the sf package (Pebesma and Bivand, 2023) to create buffers around each forest polygon, generating new polygons that expanded each forest patch by a specified radius. We applied buffers that progressively expanded or contracted the forest patch polygons in 11 km increments, resulting in 50 different forest cover scenarios. This increment of 11 km was chosen so that the scenarios varied from the baseline of 16.7% of forest cover (the empirical scenario) to a minimum of 2.59% of forest cover and to a maximum of 98.8%. (Fig. 2).
Scenarios illustrating the complexity of the landscape by varying the natural and restored forest cover, northeastern São Paulo state, Brazil ((a)- empirical landscape with 16,7% of forest cover, (b) – simulated deforestation with 6,3% of forest cover and (c) – simulated reforestation with 36,8% of forest cover). Forest cover is depicted in green and sample points (trap locations and nodes in the spatial network) in red. Forest cover data was provided by MapBiomas, Collection 5.
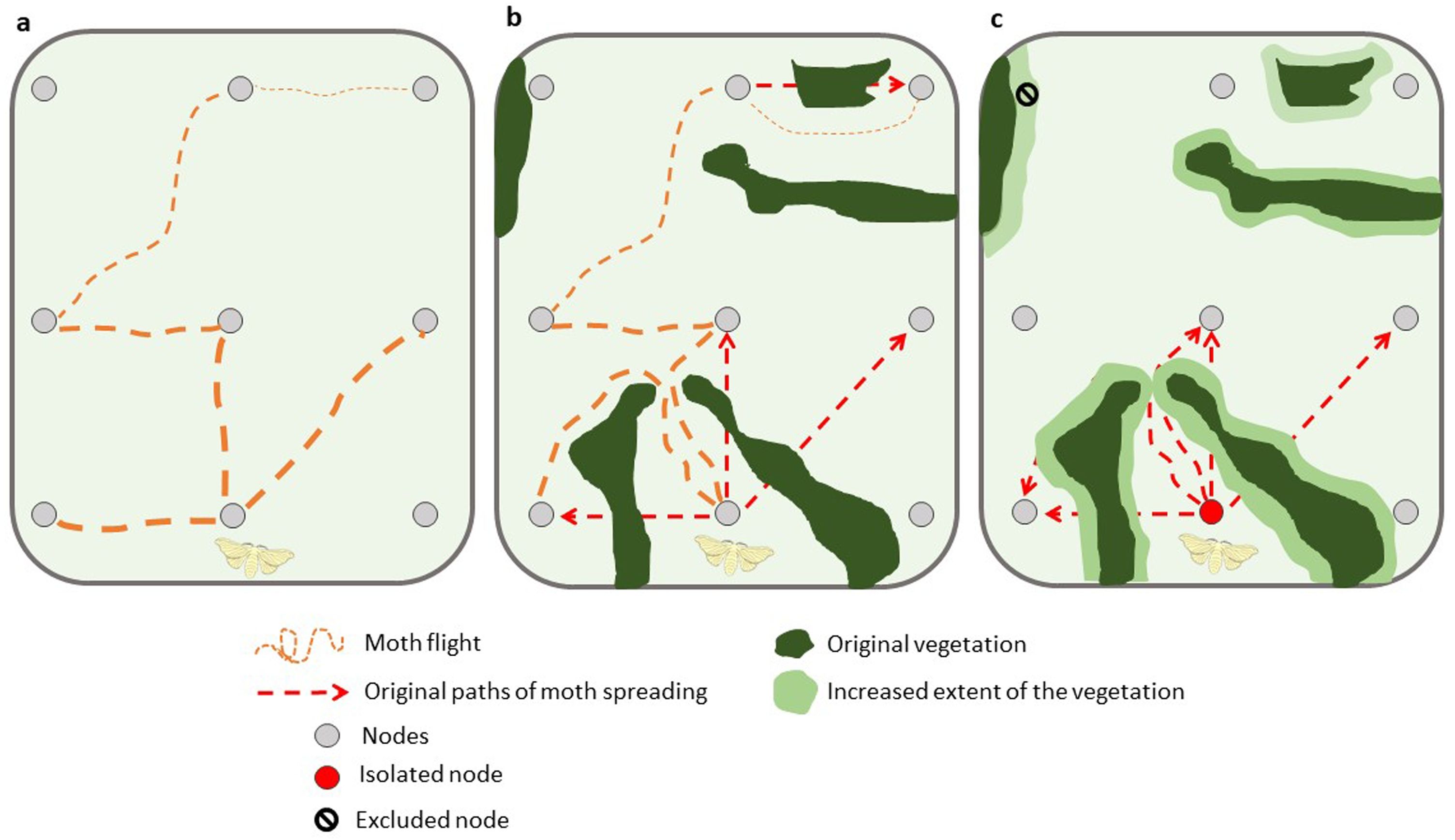
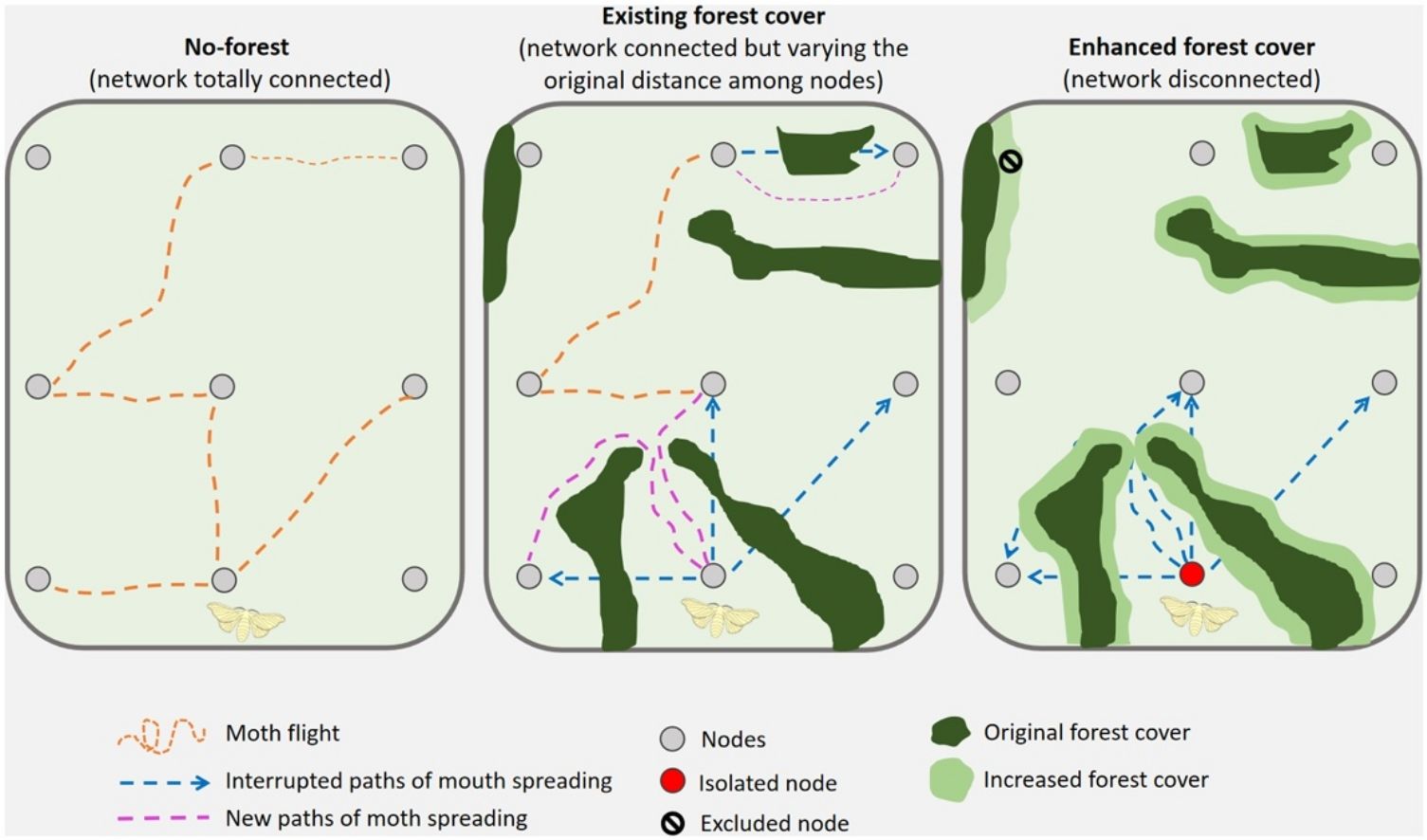
We build spatial networks based on landscape data using the following algorithm: (1) Each sample point (i.e., monitoring trap) is depicted as a node and we directly connected all nodes to one another across the landscape, as would be the case if there were no barriers to pest dispersal, i.e., a landscape with no natural or restored forest patches (Fig. 3a). (2) We assigned to each link a weight, dij. If there were no patches of natural or restored forests, dij is the Euclidean distance between two nodes The Euclidean distance was computed after rasterizing the shape files of the empirical landscape into a 500 × 500 grid. (3) If, however, there were patches of vegetation (natural and restored forests) between two nodes, we assumed they prevent direct dispersal. In this instance, we computed the shortest direct distance between the two nodes assuming movement around the habitat patch perimeter (Fig. 3b). To compute the distance between two nodes assuming movement around the habitat we first rasterized the shape files of the landscape into a 500 × 500 grid. Next, we built a transition matrix assuming that each point in the grid can access its 8 nearest neighbors. In this transition matrix the cost of moving from one point to the other corresponds to the physical distance between points. However, we set an infinite cost for any movement passing through a terrain contained within a polygon of natural or restored forest patch, turning these patches into impassable terrains. Finally, we used the function costDistance of the R package gdistance to compute the least-cost path between points whose coordinates in the 500 × 500 grid matched the spatial location of the monitoring traps of the agricultural system. (4) If a node was completely surrounded by vegetation, then it is isolated from all other nodes in the network with the exception of those within the same vegetation boundaries (Fig. 3c). The spatial networks produced by this approach can then be used in subsequent modelling to understand how management, restoration and conservation can influence the movement and pest spread across a landscape.
Conceptual diagram representing the spatial network in three hypothetical landscapes varying in complexity: (a) no-forest – network totally connected. A subset of all potential connections is represented, (b) existing forest cover – network connected but varying the original distance among nodes and (c) enhanced forest cover – network disconnected. In the diagram we assumed one starting node for moth spreading. The thickness of the path of moth spreading represents the effect of the distance among nodes.
We used the location data from D. saccharalis monitoring traps (see SI Traps dataset) to construct a weighted spatial network for each forest cover scenario. These networks represent the potential pathways of pest dispersal (see Spatial network approach). In the spatial network, each sampled point (trap location) is depicted as a node and two nodes are connected to each other by a link that describes the potential for dispersal of D. saccharalis between both points. Each forest cover scenario resulted in a different spatial network configuration affecting pest spread.
To characterize the structure of spatial networks we used two network metrics (Costa et al., 2007) that are associated with how quickly a pest can disperse from a node to another: (1) weighted average shortest path length (in km) among nodes. Averaging all shortest paths among nodes allowed us to quantify how varying the complexity of the landscape affects the average distance that a pest needs to travel to reach other nodes in the landscape. We computed the weighted average shortest path length as the harmonic mean of the shortest paths in the spatial network (Costa et al., 2007):
N corresponds to the total number of nodes in the network and dij corresponds to the weighted shortest path between node i and j (i.e., the least-cost path between the two nodes in the landscape). In Eq. (1), h can also be interpreted as the inverse of the average communication efficiency in a network (Latora and Marchiori, 2001). We then computed the number of components, in which a component is a network subset containing all nodes that are directly or indirectly connected to each other. These components emerge in our spatial networks when vegetation patches surround a subset of nodes such that they are connected to each other but isolated from all other nodes in the landscape.
The number of components in the spatial networks were identified with the ‘igraph’ package in R v 4.0.0 using the function components (R Development Core Team R, 2021).
Modelling infestation dynamicsWe used a discrete time, spatially explicit, stochastic model in conjunction with the simulated spatial networks to understand how landscape complexity affects the spread of D. saccharalis across the scenarios. Our model builds upon previous work of disease spread in networks that belong to the family of spatially explicit SI (susceptible-infected) models (Allen-Perkins and Estrada, 2019; Gómez et al., 2010). In the model, we assumed that each node i in the spatial networks is either in an infested (sit = 1) or uninfested state (sit = 0) and that the pest spread through the links among nodes. These links, therefore, create pathways through which pests can disperse to other nodes. We assumed that the probability of a pest to spread from a node j to a node i (pij) depends on the state of infestation of node j (sj) and two other components.
The first component (fij) is the probability that the pest follows a given path in the spatial network. Depending on the structure of the spatial network node i can be connected to few or many other j nodes. We assumed that the probability that the pest follows the path that connects nodes i and j is proportional to the total number of connections of i, as follows:
where aij(aik)=1 if nodes i and j(k) are connected in the spatial network and aij(aik)=0 otherwise. This is equivalent to assuming that the pest uniformly spreads through each pathway in the network and that there is one contact attempt per unit time.The second component is the probability that the pest actually reaches node i from node j, rij. We assumed that this probability depends on the dispersal capabilities of the pest and decays with the geographical distance between nodes i and j:
where dij corresponds to the distance that separates nodes i and j in the landscape, and β is the distance that the pest can cover in the landscape so that if dij is very high compared to β, then the probability that the pest actually reaches node i is extremely low. In the model, we parameterized β with the maximum flight distance recorded for D. saccharalis (Urban and Keitt, 2001). Under these assumptions there are two ways that a pest can infest a node j from node i. First, if the distance between i and j is short enough relative to the dispersal ability of the pest (β), then the pest can infest node j without passing through any other intermediate nodes. Second, when two nodes are too distant from each other relative to the dispersal ability of the pest, it can only infest node i when it first infests the intermediate nodes between i and j.Combining the two components we have the probability that node i is infested by a giving node j from one time step to the other:
where sjt=1 if node j is infested at time t and sjt=0 otherwise. Under these assumptions, node i is infested by at least one other node j in the spatial network from one time step to another with total probability:where N is the total number of nodes in the spatial network and ∏j=1,j≠iN1-pijt is the probability of node i not being infected by any other node j at time t. Each time step, therefore, corresponds to an event of infestation in which any uninfested node can become infested with probability given by Eq. (5).We ran 2,000 numerical simulations of the model for each scenario of forest cover (total of 104 simulations) in the Julia programming language v 1.5.3 (Bezanson et al., 2017). Each simulation began with one random node being assigned as the initial focus of infestation (Electronic Supplementary Material, Fig. S1); however, we also tested the robustness of this assumption through a set of simulations in which there were multiple foci of infestation (Electronic Supplementary Material, Fig. S2). Then, we iterated the model for 30,000-time steps. Each time step corresponds to an event of infestation, i.e., an event in which adult male moths disperse across the landscape. During each simulation we recorded the time step at which each node was infested and at the end of the simulation we recorded the proportion of infested nodes. Since in our model nodes are not able to get uninfected, all nodes that can be reached by at least one pathway from the initial focus of infestation eventually get infected given enough time steps. The number of time steps used was enough for approximately 50% of the nodes to get infected in the null scenario, in which there is no forest cover. Thus, we used this number of time steps as a benchmark to understand how increasing forest cover could slow down the spread of the pest or prevent nodes from being reached from the initial focus of infestation.
Predicting infestation trajectoriesIn networks, the direct pathways of one node can cascade to other nodes via indirect pathways. For instance, in our model node j can directly infest node i which, in turn, can infest another node k. These cascades across indirect pathways are a ubiquitous feature of networks that shape several ecological processes, from coevolution to extinction cascades (Guimarães et al., 2017; Pires et al., 2020). Thus, we tested whether direct and indirect pathways among nodes in each spatial network can be used to predict the trajectory of the infestation in our numerical simulations.
First, we computed a matrix of direct pathways (P) whose elements (pij) represent the probability that a given node i is directly infected by node j (Eq. (5)). From this matrix we extracted the weight of the direct pathways of the node initially assigned as the focus of infestation, k, in each simulation to each node i in the network, pik (herein referred as Piin). Then, we used the P-matrix to compute a matrix of both, direct and indirect pathway, T-matrix. In this matrix the entry Tij contain information about the pathways of a given node j to another node i not only directly, but also indirectly through all other intermediate nodes. The T-matrix can be obtained by the powers of matrix P. For instance, if pij(2) is an element of matrix P², pij(2) represents the pathways connecting the node j to node i through pathways of length 2, e.g., through an intermediate node. The sum of the powers of matrix P, representing all possible pathways of all lengths l, ∑l=1∞Pl, converges to a matrix T=I-P-1, in which I is the identity matrix (Guimarães et al., 2017; Katz, 1953) describing the sum of direct and indirect pathways that each node has on each other. From the T-matrices calculated for each simulation we extracted the total direct and indirect pathways that the initial focus of infestation k exerted in each node i in the network, Tik (herein referred as Tiin).
Next, we used Random Forests to evaluate the efficacy of direct (Piin) and indirect (Tiin) effects in predicting the time step at which a given node was infested in our numerical simulations (details in Box 1).
Random forests: description and analysis procedure.
Random Forests are ensemble machine learning algorithms that use bootstrap aggregations of decision trees (Cutler et al., 2007). The algorithm constructs and averages the models of N decision trees which are grown by resampling the data with replacement. Random forests are unaffected by the scale and distributions of both response and predictor variables, and have been used as a reliable predictive tool for answering ecological questions (Cutler et al., 2007). To fit the Random Forest model, we performed four main steps: (1) We randomly selected 50 simulations from the 2,000 simulations ran for each forest cover scenario (see Numerical simulations). (2) We merged the results of these 50 simulations into a single dataset containing simulations in which each of the 1089 points were infested at a different time and there was a different initial focus of infestation. (3) We randomly split this dataset into a training (70% of the dataset) and a test set (the remaining 30% of the dataset). Using the training data, we fitted a Random Forest model with 500 decision trees in which we used the time at which point i was infested as response variable and Piin, Tiin, and the ID of the initial focus of infestation as predictors. (4) We repeated this procedure 100 times for the results of each different scenario of forest cover (total of 5000 Random Forest models).
This approach allowed us to test and measure the variation in the efficacy of models fitted to a wide range of initial simulation conditions. Of all the possible initial conditions (i.e., patch as initial focus of infestation), our approach covered at least 97% of all possibilities (sample coverage of at least 1061 of 1089 points as initial focus in each scenario of forest cover). We evaluated the efficacy of the predictions of each model through the coefficient of determination (R2) between model predictions and the actual values of the response variable in the test data. To determine the importance of each predictor variable to the efficacy of model predictions, we used the percentage increase in mean square error when the model is trained with a randomly permuted version of the predictor variable (Cutler et al., 2007). The models were fitted in R v 4.0.0 (R Development Core Team R, 2021) with the ‘randomForest’ package using the function randomForest() and for all parameters was used the default, except for ntree = 500 (Breiman et al., 2018).
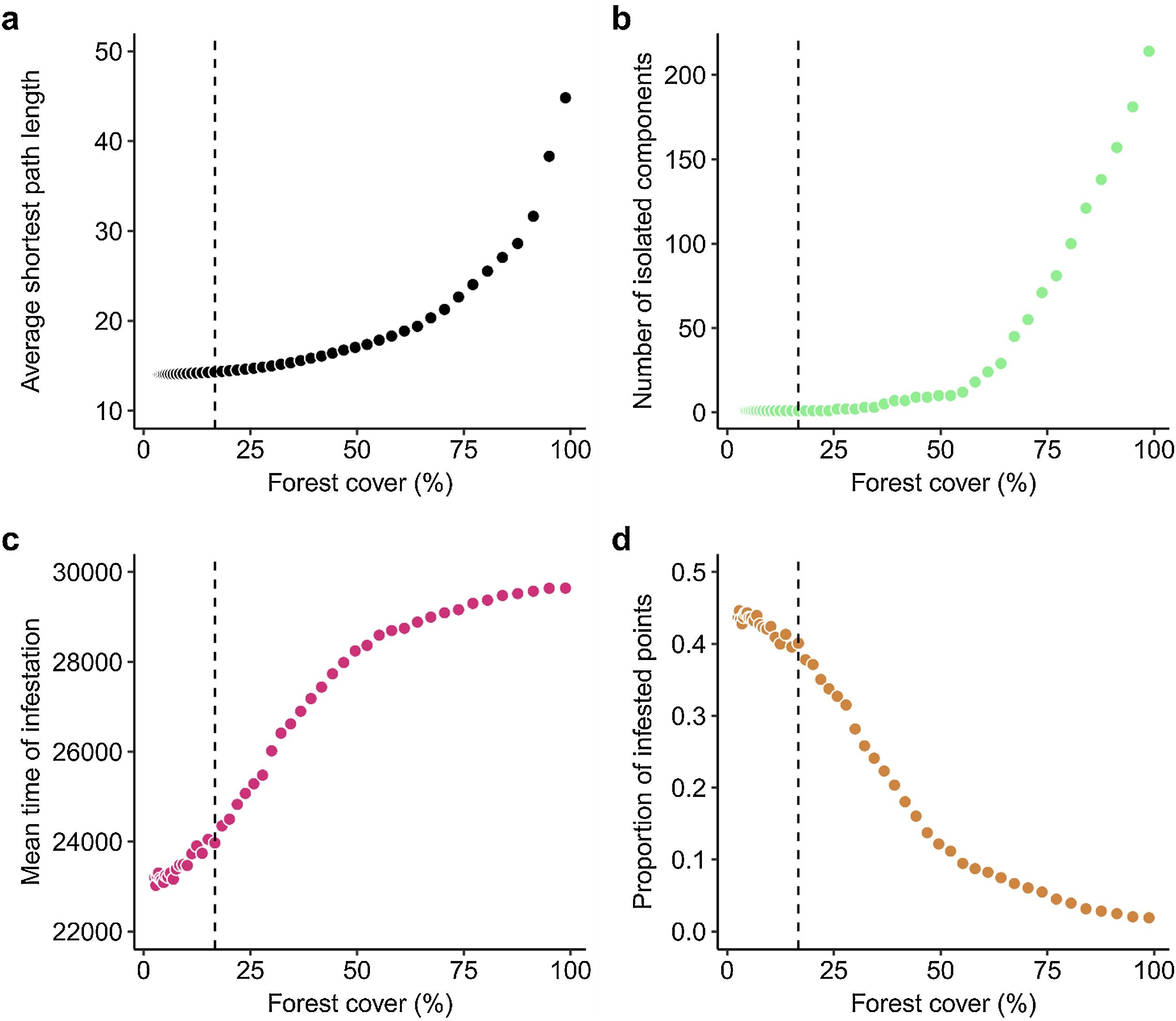
ResultsAverage shortest path length and the number of components in the spatial network increased with forest cover (Fig. 4). Our analysis revealed that as the percentage of forest cover on the landscape increased, the values of the metrics we measured did not increase linearly. Instead, the metric values exhibited an exponential relationship. This means that small increases in forest cover at higher percentages resulted in disproportionately large increases in the values of spatial network metrics, highlighting the exponential nature of the relationship. This suggests that high levels of forest cover have a greater impact on spatial network metrics, more so than lower levels of forest cover. For instance, increasing the percentage forest cover from the 16.7% to a scenario with 25.8% resulted in an increase in the average shortest path length from 14.31 to 14.72 km. In contrast, when percentage forest cover increases from a scenario with 25.8 to 49.5%, and from 49.5 to 77.11%, the average shortest distance increases from 14.72 to 16.40 km and from 16.40 to 24.04 km, respectively (Fig. 4a). Similarly, the number of components in the spatial network of the agro-ecosystem increases from a single connected component at 16.7% forest cover to 2 different components at 25.8% of forest cover. However, the number of components increases from 2 to 10 and from 10 to 81 when land cover increases from 25.8 to 49.5% and from 49.5 to 77.11%, respectively (Fig. 4b). Therefore, increasing the percentage forest cover can substantially increase the distances that pests need to cover to disperse to other points and the number of locations that pests cannot reach in agro-ecosystems, as illustrated by breaking the landscape in two components at 25.8% of cover.
Forest cover in the landscape affects (a) the average shortest path distance among points (in km2); (b) the number of isolated components in agro-ecosystems spatial networks; (c) the mean time of infestation and (d) the proportion of infested nodes. The dashed line indicates the empirical scenario with 16.70% of percentage of vegetation cover. In (b)–(c) points correspond to the average values of the 2000 simulations ran for each scenario.
Through numerical simulations of a stochastic model of pest infestation we found that increasing the percentage forest cover of the landscape slowed down the spread of pests and decreased the number of nodes in the agro-ecosystem reached by the pest infestation (Fig. 4). This effect is weaker in increasing the mean time at which nodes were infested (Fig. 4c) and stronger in decreasing the proportion of infested nodes at the end of simulations (Fig. 4d). For instance, almost doubling the percentage land cover, from 16.70 to 34.43%, meant that the mean time of infestation weakly increased from 23970 ± 6 (mean ± SE) time steps to 26619 ± 5, whereas the proportion of infested nodes decreased by 40%, from 0.40 ± 0.01 to 0.24 ± 0.01. Similarly, almost doubling the forest cover again from 34.43 to 67.26% increases the mean time of infestation to 28995 ± 3, whereas decreases the proportion of infested nodes to 0.06 ± 0.01. Therefore, when the percentage of forest cover in the landscape increases, pest infestations slow down and reach a smaller number of nodes. Further analysis showed that the standard deviation of the times of infestation also increased with forest cover (Electronic Supplementary Material, Fig. S3). Such effect occurs because an increased forest cover prevents multiple nodes from becoming infected at short time intervals. These results hold even if we vary the dispersal capabilities of the pest and the permeability of natural and restored forests (Electronic Supplementary Material, Figs. S4, S5).
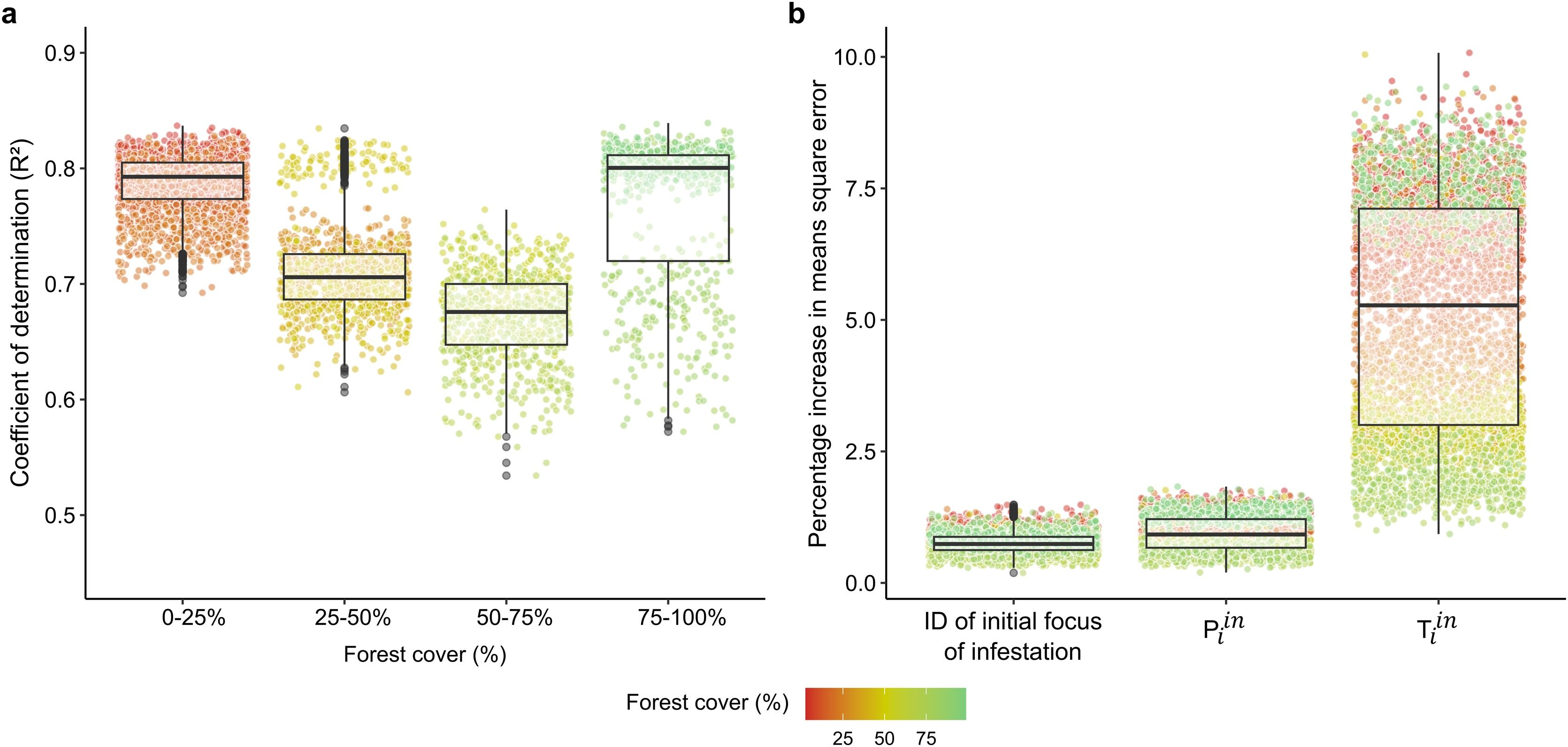
Random forests models predicted the trajectory of the infestation with up to 86.61% precision (Fig. 5a). Predictions were more precise when forest cover was less than 25% (78.67 ± 2.50% of model precision), while the least precise predictions occurred when forest cover was in between 50 and 75% (67.17 ± 3.82% of model precision). On average across all scenarios, direct and indirect pathways from the initial focus of infestation in the spatial network predicted the time of infestation of nodes with 75.85 ± 6.61% accuracy (mean ± SD). Thus, our approach predicts the trajectory of the infestation with high precision, even using a minimal set of variables (i.e., direct pathways, indirect pathways, and initial focus of infestation). However, from our predictor variables, Tiin (total direct and indirect pathways to node i) disproportionally contributed to these levels of model accuracy. Random forest models fitted with randomly permuted versions of Tiin resulted in a higher increase in mean square error when compared to Piin and the ID of the initial focus of infestation. Such comparisons were made to random permutations of each of the variables. Across all scenarios, randomly permuted versions of Tiin increased the model mean square error by amounts more than 5 times higher than Piin and the ID of the initial focus of infestation (Fig. 5b; 4.79 ± 2.15% increase in mean square error for Tiin compared to 0.93 ± 0.27% and 0.91 ± 0.26 for Piin and the ID of the initial focus of infestation, respectively). Indirect pathways were thus more important than the direct pathways and the initial focus of the infestation. That means that pathways not interacting directly can strongly influence the trajectory of pest infestations in our system. Therefore, by considering both direct and indirect pathways through the spatial networks, our model can predict with an accuracy of nearly 80% the most susceptible points to pest infestations.
Direct and indirect effects predict the trajectory of pest infestations in agro-ecosystems. (a) Coefficient of determination between Random forests predictions and actual values of the time step at which points were infested. The different categories in the x-axis include the scenarios within the intervals of forest covers depicted in these categories. (b) Increase in model mean square error when fit with a randomly permuted version of the corresponding predictor variable. Points represents the results of 100 Random forests fit for random subsets of 50 simulations of pest infestation for each scenario of forest cover in the landscape (total of 5000 Random forests models).
Combining spatial network approaches, mathematical and statistical modelling and species observation data provides an opportunity to understand ecological processes at the landscape scale. Here, we showed the utility of a spatial network approach with empirical data from a sugarcane agro-ecosystem and explored how pest dispersal across an agro-ecosystem can be influenced by landscape complexity. We found that the cover of natural and restored forests can reduce the spread of pests across simulated landscapes. Although vegetation is identified as a fundamental element of the landscape related to the pest control in agro-ecosystems (Morandin et al., 2016; Aristizábal and Metzger, 2019; Barral et al., 2015), the effects of forest cover have seldom been explicitly linked to the pattern of pest infestation.
In this study, increasing the cover of natural and restored forests in simulations of pest spreading led to increases in the mean time of infestation and decreases in the proportion of infested nodes, even simulating different permeabilities of forests in the landscape (Electronic Supplementary Material, Fig. S3). These findings show that variations on forest cover can be spatially important for pest dynamics. Several studies have previously shown that simplified landscapes (i.e., monocultures) allow specialist pest species to freely disperse, whereas landscapes composed by mosaics of natural and semi-natural habitats amid the crop (i.e., complex landscape) hamper population growth and spread (Paredes et al., 2021; Medeiros et al., 2019). Complexity in agro-ecosystems more generally is associated with higher densities of natural enemies and lower pest density (Paredes et al., 2021; Martin et al., 2019; Aristizábal and Metzger, 2019; Breiman et al., 2018; Medeiros et al., 2019; Andow, 1983; Meehan et al., 2011). For example, ant species colonizing forests are recognized as important natural enemies of pests in sugarcane crops contributing to population control (Santos et al., 2018). Studies have empirically shown that 30–40% of the forest cover should be preserved or restored in the landscape to maintain forest-dwelling populations of natural enemies (e.g., birds, frogs, mammals and ants) (Andren, 1994; Arroyo-Rodríguez et al., 2020; Banks-Leite et al., 2021) and a balance between the delivery of goods and services to humans and the protection of biodiversity and wildlife (Arroyo-Rodríguez et al., 2020). Nevertheless, the current levels of restoration of natural and semi-natural habitats may not be enough for the enhancement and persistence of biodiversity and generation of ecosystem services beneficial for agriculture (Boscolo and Metzger, 2011; Rother et al., 2018). Our models suggest that further increasing forest coverage is required to effectively arrest the spread of pests. For example, increasing current forest coverage by at least 9% can significantly increase the distances that pests need to travel to disperse to other points in the agroecosystem, which could help reduce the pest spread. While active forest restoration has already been implemented in the landscape we studied (Rother et al., 2019), our findings indicate that additional forest restoration could help avoid the high levels of pest infestation and crop loss observed in more simplified landscapes. This would also potentially reduce the economic cost of pest control (Meehan et al., 2011). More research is however necessary to validate these findings and to explore the integration of natural enemies’ habitats into pest management strategies.
We also found that the effect of forest cover increases in slowing down the spread of pests can be viewed as changes in the spatial network in the agro-ecosystem in which a pest is spreading. In diversified landscapes, the distance among suitable crop stands and the number of habitat boundaries between them is high relative to simplified landscapes. As such, complex agro-ecosystems represent a challenge for pests to locate host plants and survive (Bonte et al., 2012). Some studies argue that diversification in agricultural landscapes can mitigate the loss of biodiversity, promote ecosystem services and reduce the costs of pest control (Paredes et al., 2021; Tamburini et al., 2020). For instance, forests embedded in the agro-ecosystems can increase landscape permeability and offer complementary resources to forest-dependent species, which in turn can provide ecosystem services to agriculture (e.g., pest control and pollination) (Grass et al., 2019; Mendenhall et al., 2016). It remains, however, a challenge to find the optimal level of forest cover that balances ecological and economical values to design more biodiversity-friendly landscapes (i.e., landscapes containing stepping stones, isolated trees, strips, or even hedgerows) (Barbosa et al., 2017).
By understanding the direct and indirect paths connecting nodes we show that it is possible to predict the trajectory of pest infestation across spatial networks connecting the landscape. Our spatial network approach can: (i) contribute to the understanding of the spread of pests and the potential effects of landscape simplification (e.g., low forest cover and connectivity) on the patterns of pest infestations; and (ii) be used to predict the locations in the landscape that are most susceptible or at risk from pest infestation. Identifying and monitoring the sites that are likely to be infested could provide an early warning of pest occurrence. Furthermore, early protective measures in these same sites would minimize the spread of the pest (Pires et al., 2017). Finally, this framework could be extended to quantify other aspects of the spatial network that would be pivotal to pest spreading, such as connections between otherwise isolated sections of the network.
In the context of integrated pest management, the approach introduced here is particularly attractive as it requires only information on the distance among points and the dispersal capabilities of organisms. Despite its limitations, which include oversimplification of biological factors, data dependency, scale sensitivity, and challenges in capturing the dynamic and heterogeneous nature of agricultural systems, we envision that these methods can be further developed. This development aims to enhance our understanding of the spread of various crop pests in diverse landscape contexts worldwide. Moreover, it seeks to explore how ecosystem services, facilitated by a variety of species interactions within ecological networks, can be effectively leveraged (Miller et al., 2021). In a practical view, forest cover (whatever the mechanism by which it impedes dispersal) can effectively be used to control pest occurrence in the network, providing a real tool that managers can use. By enhancing biodiversity, creating barriers to pest movement, supporting natural predators, and increasing ecosystem resilience, habitat restoration in agroecosystems provides a multifaceted approach to managing pests sustainably. As climate change continues to alter pest dynamics, the importance of healthy, restored ecosystems cannot be overstated. Given the demand for food production and the need to conserve ecosystems, such an approach has the potential tool to: (i) find a balance among yield productivity, cost of pest control, forest conservation and ecosystem services provision in agro-ecosystems; (ii) provide scientific evidence to guide conservation and restoration plans; and (iii) contribute to public policy discussions in the field of sustainable agriculture.
CRediT authorship contribution statementDCR, LGC, JT, FMW, MD, DME, PRG: Conceptualization, Methodology. DCR: Data curation, Investigation, Formal analysis, Writing-Original draft preparation. LGC: Methodology, Software, Formal Analysis. DME: Funding acquisition. PRG: Supervision. DCR, LGC, JT, FMW, MD, DME, PRG: Writing- Reviewing and Editing.
Data availabilityAll code used to complete the analyses in this study is available at https://github.com/lgcosmo/Rother_et_al_pest_spread_agricultural_systems.
Data were provided by company and as such are not publicly available.
We hereby certify there is no conflict of interest related to our work.
We thank the sugarcane company (that wishes to remain anonymous) for providing the data on moth traps, and The Royal Society, London for the financial support granted to DCR, JT, FMW, MD, DME and PRG (CHL\R1\180156). LGC thanks FAPESP for a PhD fellowship (#2019/22146-3). PRG thanks FAPESP (#18/14809-0) and CNPq.