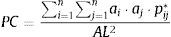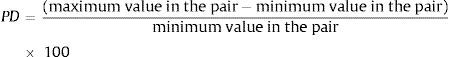Evaluating the impacts of large infra-structure projects on biodiversity is challenging, especially for linear projects such as power lines, which may extend over large geographical areas. Here we show how landscape metrics can be easily incorporated into Environmental Impact Assessment to identify the best alternative location for implementing linear infrastructures. To do so, we evaluated as a case study three alternative paths presented in the Environmental Impact Assessment of a power line in the Brazilian Atlantic Forest. For each path, we calculated habitat availability – an integrative metric that combines habitat amount and connectivity – for eight hypothetical species, and four complementary metrics for comparison (habitat amount and number, size and isolation of habitat patches). Habitat availability varied substantially among alternative paths, being up to 46% higher for one path compared to another one. Complementary landscape metrics varied little among alternative paths, and did not converge for the same results of habitat availability, most likely because these metrics do not consider connectivity, a critical ecological attribute of landscapes affected by power lines. Our results indicate that habitat availability can be a useful metric to inform landscape-level decision-making involved in Environmental Impact Assessment, particularly in transmission line projects.
Environmental Impact Assessment (EIA) was first formally established in the USA approximately fifty years ago, and is now considered an essential instrument for environmental policy and decision-making (Glasson et al., 2013). Since its establishment, the contents and methods of EIA have been debated, revised and improved, incorporating new approaches and matching the study to the type of project that is under evaluation (Lallier and Maes, 2016; Mishima et al., 2016). Nonetheless, it remains a challenge to evaluate the impacts of many projects due to the variation in their characteristics, such as the attributes of the directed affected area, the type of pollution generated, and the overall size of the project.
Large linear projects, such as railways, highways and power lines, have been expanded at high rates in the last decades worldwide (Kleinschroth et al., 2016; Teixeira et al., 2016). These types of infrastructure are not restricted to a specific landscape, rather prolonging across hundreds of kilometers through different landscapes. Therefore, larger linear projects may cause greater fragmentation of native habitats across landscapes (Geneletti, 2004), potentially leading to higher negative impacts on biodiversity (Ewers and Didham, 2006). Nonetheless, economic aspects are generally favored over ecological and environmental impacts, when choosing the location of linear infrastructures (Igondova et al., 2016). Thus, it remains a challenge to evaluate the environmental impacts of large linear projects, especially because of their effects on multiple landscapes.
In Brazil, EIAs are mandatory for all projects that potentially cause significant environmental impact (e.g. habitat loss, fragmentation and/or degradation) and must be conducted before on-site installation of infrastructure (Brazilian Constitution, Art. 225 and CONAMA Resolution n° 237/1997). These assessments, however, are frequently criticized because they sometimes lack both scientific rigor to predict the impacts on biodiversity and technical and locational alternatives to reduce these impacts (Ministério Público Federal, 2004; TCU-Tribunal de Contas da União, 2004). For such projects, spatially-explicit analyses could provide critical information to assist decision-makers assessing the ecological, economic and social impacts of each alternative location. However, quantitative spatial analyses are still rarely included in EIAs, even when aerial imagery and maps are available, in part due to uncertainty regarding the better methods and metrics to quantify spatial patterns.
Recently, Koblitz et al. (2011) proposed that EIAs should incorporate landscape ecology concepts to improve the decision-making process regarding the environmental/ecological viability of large projects. Landscape ecology concepts and tools can be particularly useful for linear projects, as they can be applied over large geographic areas (Teixeira et al., 2016). Nonetheless, the application of landscape ecology concepts and metrics to assist decision-making is still rare in EIAs (e.g. Igondova et al., 2016). In this sense, the concept of “habitat availability” (sensuSaura and Pascual-Hortal, 2007) could be especially useful in EIAs to assess the impacts of different locational alternatives. Habitat availability (HA) refers to the amount of habitat that is accessible by a species in a landscape, and depends on both habitat amount and habitat connectivity. Because it combines these two elements, HA provides an integrative and ecologically meaningful concept and metric for landscape analysis, and, as a result, has been increasingly applied to guide decision-making in conservation and restoration actions (e.g. Crouzeilles et al., 2015, 2014, 2013; Tambosi et al., 2014; Tambosi and Metzger, 2013). HA could be useful for EIAs because it can be used to quantify landscape changes across large geographical areas, using relatively simple graph-based algorithms (Pascual-Hortal and Saura, 2006; Saura and Pascual-Hortal, 2007).
Here we show how HA and other landscape metrics can be incorporated into EIAs to identify the best location for projects with large linear structures. To do so, we contrasted the response of eight hypothetical species with different dispersal abilities to three alternative paths of a new overhead power line to be installed within the Brazilian Atlantic Forest. For each path, we calculated HA and four complementary and widely used landscape metrics: total habitat amount, number of patches, patch size, and patch isolation. We show how HA can help decision-making to identify the best ecological alternative path for linear structures.
Material and methodsStudy areaTo illustrate our approach, we used as a case study the EIA of a project composed of three Power Transmission Lines (TL), TL 500kV Araraquara 2 – Itatiba, TL 500kV Itatiba – Bateias and TL 500kV Araraquara 2 – Fernão Dias, to be installed in the states of São Paulo and Paraná, Brazil. The project will transmit energy from the Electrical Substation Araraquara 2 to three other substations, but consists, actually, of two distinct and uninterrupted lines, as the TL 500kV Itatiba – Bateias is a continuation of the former TL 500kV Araraquara 2 – Itatiba. The summed length of these power lines is 885km, with a 60-m large right-of-way corridor along most of their length. In the sections where TL 500kV Araraquara 2 – Itatiba and TL 500kV Araraquara 2 – Fernão Dias are parallel, however, a 110-m large right-of-way corridor will be established. The project is being evaluated by the Brazilian Institute of Environment and Renewable Natural Resources (IBAMA), which has received the EIA in April 2015. IBAMA gave a Previous License in November 2015 that attests the project as environmentally viable, and authorized the installation in March 2016 (all data is public and provided in the Administrative Process number 02001.000480/2014-38, which transacts in IBAMA). The EIA contents can be found in http://licenciamento.ibama.gov.br/Linha%20de%20Transmissao/LTs%20Itatiba-Bateias,%20Araraquara%20II-Itatiba%20e%20Araraquara%20II-Fern%C3%A3o%20Dias%20e%20Subesta%C3%A7%C3%B5es/, accessed in November 2016.
Three alternative linear paths were proposed for this project (see the kml files in Supplementary Material). The alternative 1 was used as a basis to delineate the other two paths (EIA, Vol. 1, Chapter IV). The three paths were evaluated in the original EIA using a multi-criteria quantitative comparison of the impact in two biotic, two physical and two social environmental attributes. The biotic attributes were “interferences in forest fragments” and “interferences in protected areas” (IUCN classes I–VI). The former is described in EIA as the number of forest fragments with higher probability of having its vegetation suppressed, whereas the latter is described as the length of each alternative overlapping protected areas.
To define the geographical limits for the landscape-level analysis of each path, we built a buffer of 1km radius around each alternative path. Then, we removed all forest areas located within a 60m strip along the TL path, corresponding to a 30-m band from each side of the TL. This 60-m strip corresponds to the right-of-way area, which is the area that can be used for total or selective vegetation logging. In the sections where the TL 500kV Araraquara 2 – Itatiba and TL 500kV Araraquara 2 – Fernão Dias are parallel, we removed forest areas located within a 110m strip, corresponding to the summed right-of-way strip proposed in the project (EIA, Vol. 1). Although part of the right-of-way area may remain forested after the TL installation, we considered that this area is a reasonable approximation for all the vegetation intervention needed for the installation. This intervention is a sum of forest cutting for the cables and tower installation, cables and tower security (which results in selective logging of some arboreal individuals), and vegetation cutting for new roadway access into forest fragments. Forest fragments data were obtained from the map produced by SOS Mata Atlântica and INPE (2013), available at a scale of 1:50,000 in vector format, and including forest fragments >3ha. All geographic information system data were converted to Albers projection to assure accurate area and distance calculations.
Landscape metricsTo compare how the three alternative paths could affect landscape structure, we first quantified HA (Saura and Pascual-Hortal, 2007). HA has been used as a unifying concept in landscape ecology, providing a simple and robust measure of the amount of habitat that is available for species in landscapes (e.g. Almeida-Gomes et al., 2016; Crouzeilles et al., 2014; Saura and Rubio, 2010). HA is positively correlated with species occurrence in fragmented landscapes (Awade et al., 2012), as well as a good approximation method of metapopulation capacity (Crouzeilles et al., 2015), thus serving as an ecologically meaningful metric to evaluate environmental impacts.
We calculated HA using the Probability of Connectivity index (PC; Saura and Pascual-Hortal, 2007):
where n represented the number of forest fragments in the landscape, ai and aj represented the sizes of a given pair of fragments, Pij* represented the maximum probability of connection between fragments i and j, and AL2 represented the square of the total landscape area (Saura and Pascual-Hortal, 2007). The maximum probability of connection (Pij*) was calculated considering all possible paths between the patches i and j. To calculate Pij*, we used information on the Euclidean distance between each pair of patches, and information on the dispersal ability of each species. This index varies from 0, when there are no habitat patches in the landscape, to 1, when the entire landscape is occupied by a single habitat patch (Saura and Pascual-Hortal, 2007).For a comprehensive analysis, we considered eight hypothetical species with different dispersal abilities: 5, 10, 50, 100, 150, 200, 500 and 1000m. These dispersal abilities corresponded to a probability of 50% of directly dispersal between two patches, based on a negative exponential function (see Saura and Pascual-Hortal (2007) for details). HA was calculated in Conefor Sensinode 2.5.8 command line version (www.conefor.org; Saura and Torné, 2009).
To better understand how each alternative path affects landscape structure, we also calculated four complementary landscape-level metrics: (i) total habitat amount (i.e. forest cover), (ii) number of habitat patches, (iii) mean patch size, and (iv) mean patch isolation. All metrics were calculated using only the forest fragments (considered as habitat in this analysis) that remained after the removal of the right-of-way strip for each alternative path. Habitat amount was calculated as the remaining percentage of the studied area covered by forest fragments. Mean patch size was the average size considering all forest fragments, and mean patch isolation was the mean Euclidean distance among all forest fragments (as in Crouzeilles et al., 2014). These metrics were calculated in R 3.3 (R Core Team, 2016).
Finally, to compare quantitatively how each path affected each metric, we calculated the proportional difference (PD) in each metric between each pair of paths, as follows:
The higher the PD, the higher the difference between the two paths for a given metric. We also compared patch size and isolation among the three paths using the Kruskal–Wallis test (as values were not normally distributed) in R 3.3. It was not possible to statistically test for differences in the other metrics among paths because there was only a single value per path.
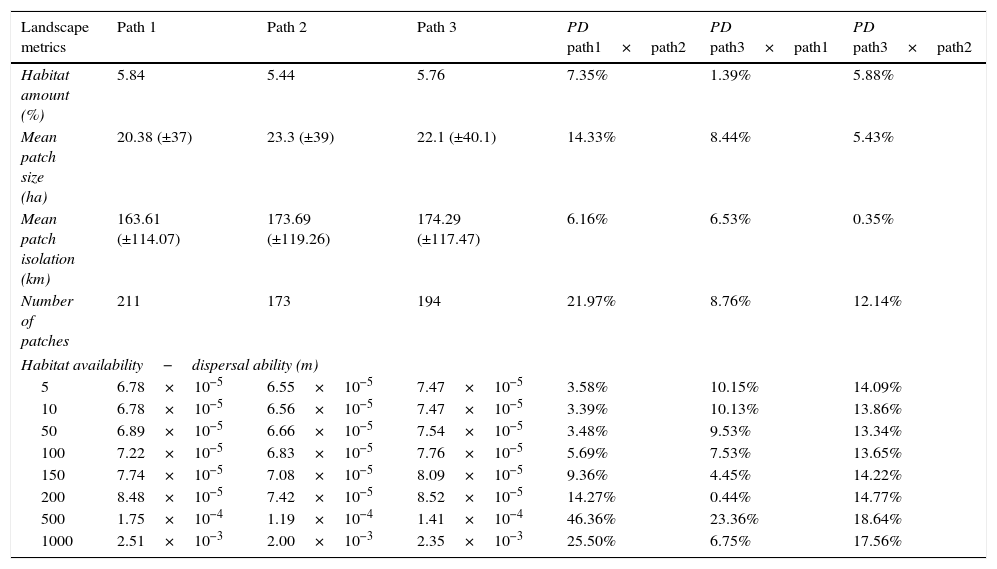
ResultsHA was relatively low (<0.003) for all species and paths (Table 1). Path 3 had higher HA for species with low dispersal abilities (<500m), whereas path 1 had higher HA for species with high and intermediate dispersal ability (≥500m; Table 1). Path 2 had the lowest HA for all species. Moreover, HA was the landscape metric with higher proportional difference for all pairs of paths (Table 1). For example, HA was 46% higher in path 1 compared to path 2, for a species with 500m of dispersal ability, whereas the same paths differed only by 6–22% in habitat amount or in the number, size and isolation of patches (Table 1).
Comparison of habitat availability and four complementary landscape metrics among three alternative paths of a power transmission line project in the Brazilian Atlantic Forest. The last three columns show the proportional difference (PD) in each landscape metric between pairs of alternative paths. PD was calculated as ((maximum value in the pair−minimum value in the pair)/minimum value in the pair)*100.
| Landscape metrics | Path 1 | Path 2 | Path 3 | PD path1×path2 | PD path3×path1 | PD path3×path2 |
|---|---|---|---|---|---|---|
| Habitat amount (%) | 5.84 | 5.44 | 5.76 | 7.35% | 1.39% | 5.88% |
| Mean patch size (ha) | 20.38 (±37) | 23.3 (±39) | 22.1 (±40.1) | 14.33% | 8.44% | 5.43% |
| Mean patch isolation (km) | 163.61 (±114.07) | 173.69 (±119.26) | 174.29 (±117.47) | 6.16% | 6.53% | 0.35% |
| Number of patches | 211 | 173 | 194 | 21.97% | 8.76% | 12.14% |
| Habitat availability−dispersal ability (m) | ||||||
| 5 | 6.78×10−5 | 6.55×10−5 | 7.47×10−5 | 3.58% | 10.15% | 14.09% |
| 10 | 6.78×10−5 | 6.56×10−5 | 7.47×10−5 | 3.39% | 10.13% | 13.86% |
| 50 | 6.89×10−5 | 6.66×10−5 | 7.54×10−5 | 3.48% | 9.53% | 13.34% |
| 100 | 7.22×10−5 | 6.83×10−5 | 7.76×10−5 | 5.69% | 7.53% | 13.65% |
| 150 | 7.74×10−5 | 7.08×10−5 | 8.09×10−5 | 9.36% | 4.45% | 14.22% |
| 200 | 8.48×10−5 | 7.42×10−5 | 8.52×10−5 | 14.27% | 0.44% | 14.77% |
| 500 | 1.75×10−4 | 1.19×10−4 | 1.41×10−4 | 46.36% | 23.36% | 18.64% |
| 1000 | 2.51×10−3 | 2.00×10−3 | 2.35×10−3 | 25.50% | 6.75% | 17.56% |
Total habitat amount varied little among paths, from 5.44% in path 2 to 5.84% in path 1. The major proportional difference in habitat amount was 7.35%, obtained when comparing paths 1 and 2 (Table 1). Mean patch size was slightly larger across path 2 and smaller for path 1, but variability was large within each path and differences were not statistically significant (Kruskal–Wallis chi-squared=1.25, df=2, p=0.53). Patch isolation varied significantly among paths (Kruskal–Wallis chi-squared=91.44, df=2, p<0.001), being slightly smaller for path 1 and higher for path 3. Finally, the number of habitat patches was the highest for path 1 (211) and the lowest for path 2 (173; Table 1). After HA, the number of patches was the metric with higher proportional differences for all pairs of paths (Table 1).
DiscussionOur results show that HA can be a useful, simple and informative landscape metric to support ecological decision-making in EIAs, particularly in large linear projects. HA was the metric that captured the highest proportional difference between paths, in comparison to four other widely used landscape metrics (habitat amount, mean patch isolation, mean patch size and number of patches). This occurred because HA incorporates these diverse landscape metrics within a single metric (Crouzeilles et al., 2014). In addition, HA also considers the variation in the ability of species to move between habitat patches, which is not considered by the other landscape metrics (Crouzeilles et al., 2014; Saura and Rubio, 2010; Tambosi et al., 2014). For these reasons, we recommend the incorporation of HA to support decision-making in EIAs of linear projects.
Habitat amount varied little among paths, thus providing a weak justification for choosing any path as the best one. In addition, the path with the highest habitat amount (path 1) had lower HA for six of the eight hypothetical species analyzed, when compared to path 3. Therefore, despite habitat amount is certainly of central importance for biodiversity conservation (Fahrig, 2003), it alone might not be a helpful metric to determine the best path for linear infrastructure projects, as this metric does not take into account landscape connectivity, a critical ecological attribute affected by power lines (Andrews, 1990; Laurance et al., 2009). The increase in habitat fragmentation caused by power lines tends to be more important than the habitat loss, as the latter is usually restricted to the right-of-way corridor. On the other hand, the power line may split habitat patches or hamper individual movement across the landscape, thus reducing functional connectivity. Therefore, to properly detect the impacts of linear projects on a landscape, it is necessary to analyze landscape metrics dealing not only with habitat amount, but also with habitat configuration, especially for organisms that are unable to cross such linear elements.
Species with low dispersal ability may be especially sensitive to habitat fragmentation (Ewers and Didham, 2006), and they are likely to respond negatively to an increase in mean patch isolation especially in landscapes with intermediate (10–50%) habitat cover (Crouzeilles et al., 2014). For these reasons, one could argue that path 1 should be regarded as the best path, as it had the lowest mean patch isolation. However, this path resulted in the lowest HA for species with low (≤500m) dispersal ability. This lower HA despite the lower isolation might be explained by three factors: (i) the proportional difference in mean patch isolation among paths was low; (ii) mean patch isolation in all paths (163–164km) was much higher than the dispersal ability of species; and (iii) HA depends not only on path isolation, but also on habitat amount (Saura and Pascual-Hortal, 2007). Due to these factors, we suggest that patch isolation alone should not be used as a landscape metric to determine the best path of a power line.
Similarly, mean patch size and the number of patches, alone, can also be regarded as insufficient or even inadequate to guide decision-making. According to these metrics, path 2 was the more indicated to implement the power line, because it resulted in lower fragmentation (as judged by the smaller number of patches) and higher patch sizes, characteristics usually considered as positive for biodiversity (Ewers and Didham, 2006). However, path 2 resulted in the lowest HA for all species, probably because it had lower habitat amount, and because the difference in patch sizes among path was insignificant. Therefore, none of the four widely-used landscape metrics, alone, can be regarded as suitable for a comprehensive analysis of the impacts of linear structures on landscapes.
Even when using HA, the decision about which is the best path may not be straightforward. According to this landscape metric, in our case study path 3 would be the best for species with low dispersal ability (<500m), whereas path 1 would be the best for species with intermediate and high dispersal ability (≥500m). Which of these species should be favored for conservation? In the case of power lines, we suggest that species with lower dispersal ability should be favored, as the clear cuts created along the power lines may effectively disrupt their movement, fragmenting their populations (Ewers and Didham, 2006). In the case of roads, however, species with greater mobility may be more affected, due to road kills (Rytwinski and Fahrig, 2012). In some cases, HA analyses may indicate a single best path for all species, facilitating decision-making. If this is not the case, we recommend considering both the type of linear project as well as the composition of the local community to be affected by the project, to judge which species and paths should be prioritized.
Based on our analyses, path 3 seems to be the preference choice, as it resulted in higher HA for six of the eight species. All these species had low mobility (<500m), which make them generally regarded as sensitive to habitat fragmentation (Ewers and Didham, 2006). Coincidently, path 3 was also considered the best choice in the EIA, as the authors argued this path had lower impacts over several environment variables. However, the EIA also concluded that path 2 was less harmful when considering only the variable “interference in forest remnants” (EIA, Vol. 1, Chapter IV), contrarily to our HA analyses, which indicate path 2 as the worst for all species. The EIA is not clear on how “interference in forest remnants” was calculated, describing it as the number of forests fragments with a larger probability of having its vegetation suppressed. We believe that the use of HA analyses could have facilitated decision-making in this particular study, because it would have provided robust additional support for choosing path 3.
Our approach (comparison among alternative paths) is relevant in cases where the decision-maker wants to choose the path that leaves more remaining HA. Nonetheless, the decision-maker could also choose the path with the lower loss of HA. In the latter case, HA would also be informative, but should be calculated based on the difference between the landscape without and with the power line. This calculation is beyond the scope of this study, but may be considered in future comparisons to further compare among alternative paths for implementing linear structures.
Finally, it is important to remember that path choice for linear projects should be based on a multi-criteria evaluation, involving social, economic, physical and ecological factors, which may receive different weights by the decision-maker depending on a case-by-case analysis. Our study is focused on the assessment of ecological impacts only, which can be used in combination of social, economic and physical analysis to identify the most cost-effective patch for linear structures. In this regard, we suggest including HA analyses to assist decision-making in EIAs, as they allow the inclusion of a theoretically sound and empirically validated concept to assist identification of the best alternative location, for any mobile species in any type of landscape.
Conflicts of interestThe authors declare no conflicts of interest
We would like to thank two anonymous reviewers for valuable comments and constructive reviews.